| |
 |
Numerical Example |
 |
|
|
|
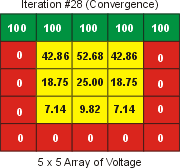
We employ the following stopping criterion: we will continue to
iteration n+1 unless the largest change in any voltage from
iteration n-1 to iteration n was observed to be less than
0.001 V. If this is our criterion, the relaxation algorithm will
stop after the 28th iteration with what should be a nearly exact
representation of physical voltages in the square: |
|
|
|
 |
|
|
|
Don't let the coarseness of our matrix sampling fool you. The
above voltages are very good models of electric potential at regularly
spaced points within our square. We can use linear interpolation
to approximate the values of voltages in between the sampled points.
In this way, we can construct beautiful voltage maps and accurate
equipotential lines, even though the sampling of our solution appears to
be rough. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2003-present Georgia Tech, all rights reserved