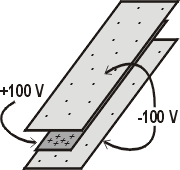
Cross-section of a Symmetrical Microstrip Line

• Technical specifics about this example.  The center strip is held at +100V and the top and bottom strips are held at -100 V.  The boundary of the region is set to 0 V.  The symmetrical microstrip line (shown below) is used on multi-layer printed circuit boards to transmit high-frequency signals with lower cross-talk and radiation than regular microstrip lines.

• Notice how the relaxation technique asymptotically converges to the true value.  The convergence slows as the number of iterations increases.

• This particular cross-section is interesting because it shows two separate "islands" of equipotential lines that grow and eventually merge.  For example, there are two rings of equipotential lines for -80, -60, and -40 V -- one on the top plate and one on the bottom plate.  The -20 V equipotential line, however, is a single ring around the entire cross-section.

• This style of microstrip line does a good job of confining its fields to within its structure.  There are very slight fringe fields around the assembly.

• The final colored voltage map may look coarse and blocky, but the relaxation technique is actually very accurate.  We can use some fancy rendering and interpolation between points to make a smoother map.  In fact, that is what the equipotential plots have done, which is why they look so smooth.