Introduction
As technologies continue to advance, it becomes necessary to innovate upon existing systems and models in order to better meet society’s changing needs. The propagation models used to design current cellular networks is no exception. These models were originally developed when in-vehicle callers were the primary end user of cellular networks – a phenomenon that is no longer the case. With most of today’s cellular activity originating indoors, the utilization of older propagation models to design cellular networks has resulted in an unacceptable level of increased uncertainty, dropped connections, and user frustration. We believe that the need to address and resolve these issues is apparent from both a commercial and forward progress standpoint. As such, this report will present an improved propagation model for the design of more efficient and effective cellular networks.
The Propagation Model
In order to construct our propagation model, we started with the basic and commonly accepted link budget equation shown in Equation 1 below [1]. We then used what we knew about propagation to make some modifications to it and began to build our model using Matlab. Following this modification step, we compared our current model to actual received signal strength data and noted any discrepancies. Subsequently, we analyzed the discrepancies between our predicted data and the measured data to form several empirically based modifications which were then ported into our working propagation model.
![]() (Eq. 1)
(Eq. 1)
PR is the power received, which is the sum of the transmit power, transmit antenna gain, receiver antenna gain, and path loss terms respectively. For the purposes of creating a model that was more effective in taking into account the effects of indoor and outdoor signal propagation, the path loss terms were of special interest.
Step One – Modifying the path loss exponent.
Most of the terms in the link budget equation are fairly set by preset operating conditions, such as frequency of operation or antenna gains. One term that was not, however, was the last term of Equation 1. This dynamic term represented the effects that the distance from the transmitter and the path loss exponent had on received signal strength. The path loss exponent in Equation 1 was given as ‘n’, and was inversely proportional to received power. In free space, n is equal to 2.0, a value that was too optimistic for our needs. We consulted a source of tabulated data showing path loss exponents for a variety of environments, and settled on an estimated n of 2.5 for our model [3]. We believed this n led to a more averaged indoor and outdoor received signal strength model than models more heavily biased towards free space propagation.
Step Two –
Adding directionality.
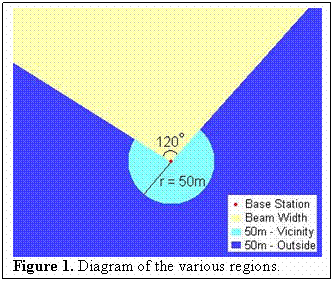
At this point we had improved upon a portion of our propagation model, but we had not yet implemented a sense of directionality. To do this, we implemented a fairly common beam width of 120 degrees into our model [2]. This meant that the full strength of the signal from the transmitter or base station would be channeled through a 120 degree spread centered at the transmit antenna’s azimuth. We also wanted to account for the signal strength not within the 120 degree beam width but still close enough to the base station to be significantly higher than more distant regions. To do this, we simply set all regions within a 100 meter radius of the base station and not within the 120 degree beam width to have a received signal strength 1 dB less than their counterparts within the 120 degree beam width. We modeled regions outside of the 50 meter radius and the beam width as having a signal strength as calculated by Equation 1 with an additional 3 dB of loss, ensuring that all distant transmitted signals not within the beam width were at less than half power. A diagram of the regions is given in Figure 1 below.
Step Three –
Testing against actual data.
We were given data for 8 IS-136 850 Mhz cell sectors operating on or near the Georgia Tech campus. Four of these sectors, denoted A – D were described in detail with base station as well as measured received signal strength data. The other four sectors, denoted E – H were described only by base station specifications.
Using the data given on sectors A – D and the predictions derived from our propagation model, we created Matlab plots of measured received signal strength versus predicted received signal strength. Performing a mean and standard deviation calculation of the discrepancies between actual and theory showed us that more modifications were in order. After comparing the measured and predicted plots, the beam width angle assumed by our model seemed slightly too small. Also, the received power within the beam width appeared to decay too rapidly in the prediction plots. Finally, the predicted received power in the areas directly adjacent to the transmitting antenna were significantly too high. These discrepancies were noted and the final modifications were made.
Step Four –
Final modifications and results.
In order to address the issues with our current propagation model, we made the following modifications:
(1.) We enlarged the beam width angle assumed by our model to 130 degrees.
(2.) After performing an empirical analysis, we determined the need to multiply the received power formulas for areas within the beam width by 0.9, effectively slowing down the rate of decay of signal strength in those regions.
(3.) More empirical analyses presented the necessity of subtracting power from the received power calculations performed by our model on areas directly adjacent to the transmitting base station.
An example of one of the m-files written to implement our propagation model is shown for Cell Sector B in Figure 2 below.
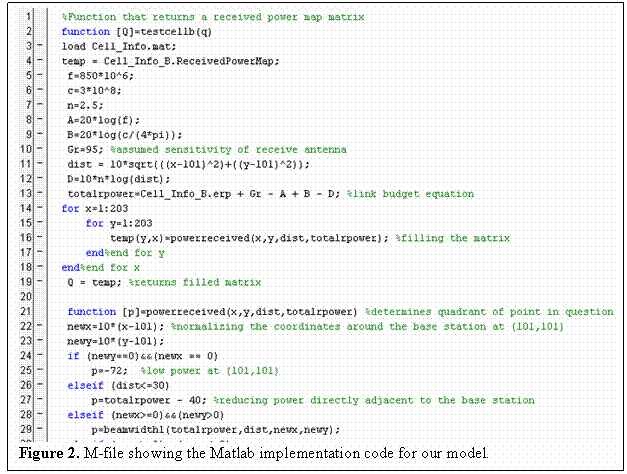

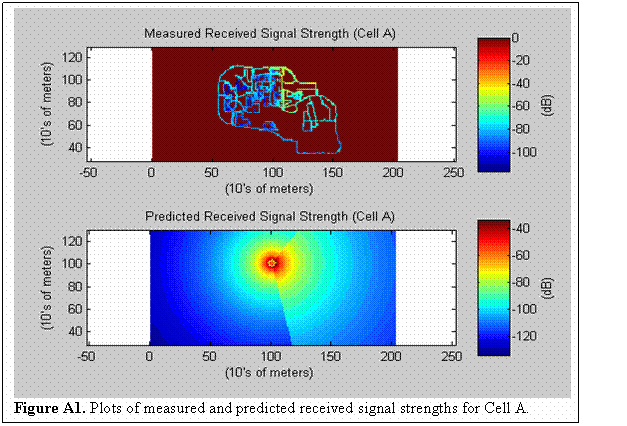
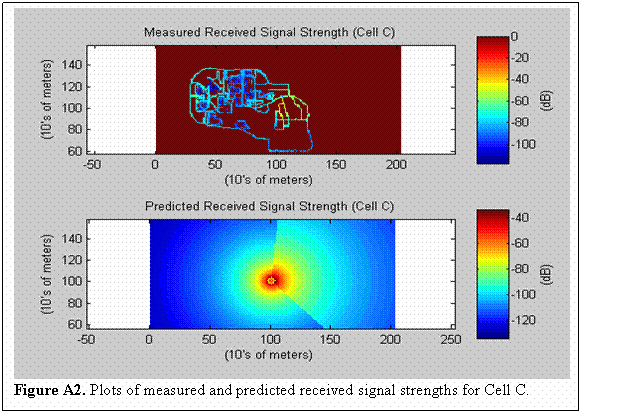
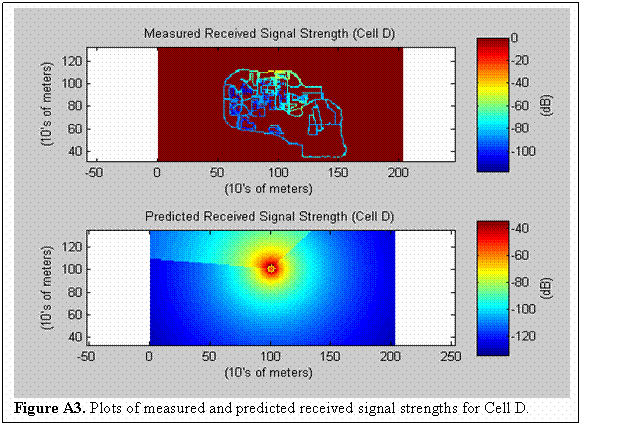
It is only necessary to show the Matlab code in Figure 2 for Cell Sector B in order to understand the inner workings of our propagation model. The m-files for Cell Sectors A – H are all fairly identical with the few discrepancies arising from calls to cell sector specific data sets, or adjustments due to azimuths changing from base station to base station. A side by side plot comparing the measured received signal strength and the predicted received signal strength for Cell Sector B is shown in Figure 3 on the next page. Similar plots as well as means and standard deviations for Cell Sectors A, C, and D can be found in the Appendix.
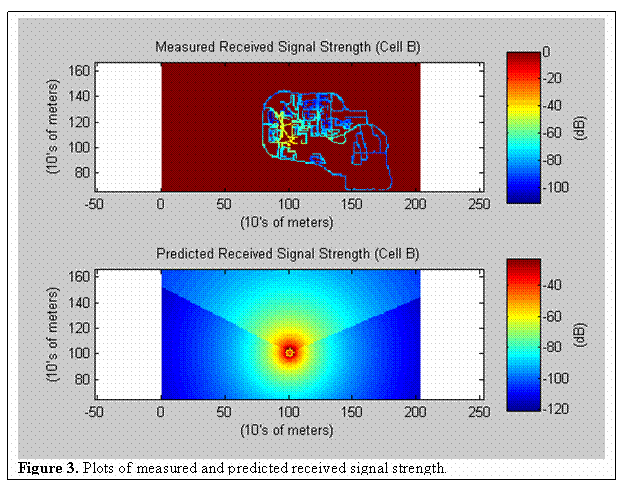
As can be seen from the plots in Figure 3, the propagation model’s behavior is generally accurate in predicting the actual received signal strength for Cell Sector B. Note that due to scaling, the colorbars and the dB values they represent are slightly different for the measured and predicted plots. The Cell Sector B prediction had an error of mean 0.67 dB and standard deviation of 14.05 dB. The mean error for this sector was excellent, but more importantly, the standard deviation could still be improved upon by further modification. This trend is repeated throughout the simulations for sectors A, C, and D, as is evidenced by a total average error of mean 8.5 dB and standard deviation of 15.4 dB for the four sites.
Conclusions
Although the propagation model we have developed is functional and is an improvement upon propagation models biased heavily towards free space operation, it could still be improved on significantly. Our model takes a smoothing, averaging approach towards determining a general picture of the received signal strength for an area with an acceptable amount of error. The next step would be to take this general picture and render it into a specific, detailed picture of predicted received power. To do this, a more comprehensive approach to modeling indoor and outdoor propagation characteristics must be used. One method would be to integrate an aggregate penetration loss (APL) feature into the existing model. APL is the ratio between average power immediately outside a building and average power immediately inside that same building [1]. In order to successfully implement an APL calculation in our model, we would need to analyze satellite photographs to determine the exact locations of buildings or other obstructions to our propagating signals. Subsequently we could initiate APL calculations everywhere in our model that the propagating signals travel from outdoors to indoors or vice versa. In addition, knowing the exact location of buildings would allow us to utilize different path loss exponents for indoor or outdoor propagation, allowing for even more accuracy. The result would be an accurately predicted RF map of received signal strength with a low standard deviation.
Despite being very accurate, however, it may not be feasible to attempt a model based on satellite photographs in terms of a nation-wide cellular network. Simply put, it would take too much time to map such a large area in such a detailed fashion. Instead, the propagation model that we have developed and described in this report would be both adequate and appropriate. Due to the smoothing and averaging nature of our model, it could successfully be implemented in a wide range of locations across the nation. However, for the modeling of those metropolitan or urban areas with a multitude of buildings, it would be ideal to add on the use of the more comprehensive approach. The bottom line is that it would be a quick and simple task to update older propagation models to our model, meaning a minimal cost in both time and restructuring. At the same time, improved coverage and decreased user frustration would spell a new era of customer loyalty and profitability. The need for new propagation models is apparent, and as cellular networks and the modern technologies that use them advance, we offer our model as the bridge between models of the past and designs of the future.
References
[1] Durgin, Greg et.Al., “Measurements and Models for Radio Path Loss and Penetration Loss in and Around Homes and Trees at 5.85 GHz,” IEEE Transactions on Communications, Vol. 46, No. 11, November 1988
[2] “EMC Antennas,” Tech Notes and Articles, April 2005 available HTTP: http://www.ramayes.com/Tech_Notes.htm
[3] Rappaport, Theodore et.Al., “Propagation and Radio System Design Issues in Mobile Radio Systems for the GloMo Project,” January 1997, available HTTP: http://www.sss-mag.com/pdf/prop.pdf
Appendix: Sector A, C, and D Results