With the increasing rate of exploration of Mars continues, data rates from Mars to Earth and back will exceed the current capacity of the DSN to probe links. Furthermore, connections to Mars terminals cannot be maintained throughout the Martian day due the obstruction of the planet itself. To alleviate the bandwidth and outage problems, MarsNet proposes a system of relay satellites orbiting Mars that handle the Earth to Martian communication.
This proposal gives the high-level overview and technical details for developing and deploying the MarsNet Martian-Aresian Relay System (MARS). In Section 1, we document the known, relevant information about. In Section 2, an overview of the system is given with the link budgets following in Section 3. In Section 4, we describe the channel access scheme, the modulation scheme, and the dynamic code allocation protocol. A detailed communication systems diagram is given in Section 5, detailing the receiving and transmitting blocks for each component in the system. Costs analysis and deployment schedule is given in the last section, Section 6.
Please note that there are many images that have been scaled down for screen space. You can click on the image for their full size and click again to return them to the smaller image.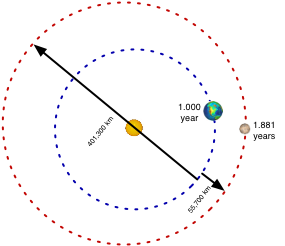 Mars' rotational period of 24.5 hours is slightly longer than that of Earth, but its revolutionary period is nearly twice totaling 686.98 days. The orbital inclination from Earth's orbital plane is 1.850 degrees. Approximately every 780 days, the Earth makes a straight line through the Sun to get to Mars. This is termed the Mars-Earth Solar Conjunction. Also, Earth's moon can block the direct line of sight (LOS) to Mars for short periods each month. The use of a solar orbiting satellite with the same elliptical as Mars but a different orbitial angle, could facilitate communication during these month-long periods of conjunction as well as the monthly occlusions by the moon.
Mars' rotational period of 24.5 hours is slightly longer than that of Earth, but its revolutionary period is nearly twice totaling 686.98 days. The orbital inclination from Earth's orbital plane is 1.850 degrees. Approximately every 780 days, the Earth makes a straight line through the Sun to get to Mars. This is termed the Mars-Earth Solar Conjunction. Also, Earth's moon can block the direct line of sight (LOS) to Mars for short periods each month. The use of a solar orbiting satellite with the same elliptical as Mars but a different orbitial angle, could facilitate communication during these month-long periods of conjunction as well as the monthly occlusions by the moon.
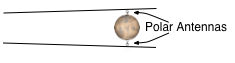
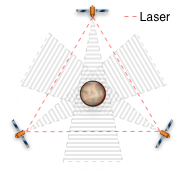 In order to fully cover the surface of Mars with minimal cost and power, three satellites and two polar antennas will be deployed to Mars. The satellites will be in an Extremely high Martian Orbit (EMO) at 778,990 km from the center of Mars. This would require a half-power beam width of only 0.5004 degrees using a 5 meter dish to cover the entire side of the planet. Any equatorial orbit would leave the poles uncovered. For that matter, no three satellites can completely cover a sphere. However, cheap, short, passive antennas can be placed at the poles that will relay signals from the uncovered polar region to the satellites. We explain our choice in orbit in Section 3.4.
In order to fully cover the surface of Mars with minimal cost and power, three satellites and two polar antennas will be deployed to Mars. The satellites will be in an Extremely high Martian Orbit (EMO) at 778,990 km from the center of Mars. This would require a half-power beam width of only 0.5004 degrees using a 5 meter dish to cover the entire side of the planet. Any equatorial orbit would leave the poles uncovered. For that matter, no three satellites can completely cover a sphere. However, cheap, short, passive antennas can be placed at the poles that will relay signals from the uncovered polar region to the satellites. We explain our choice in orbit in Section 3.4.

| G = | 4πAem | η |
| λ2 |
| Component | MARS to Earth | Earth to MARS |
|---|---|---|
| fc (GHz) | 32.05 | 34.45 |
| λ (m) | 0.0093539 | 0.0087022 |
| D (m) | 5 | 34 |
| η | 0.75 | 0.94 |
| C/N (dB) | 0.0 | 0.0 |
| GT (dB) | 63.2532 | 81.5112 |
| GR (dB) | 80.8840 | 63.8804 |
| PL (dB) | 294.6337 | 295.2610 |
| Tsys (dB) | 28 | 270 |
| B (MHz) | 150 | 150 |
| PN (dB) | -132.3667 | -122.5246 |
| PT (dB) | 18.1299 | 27.3447 |
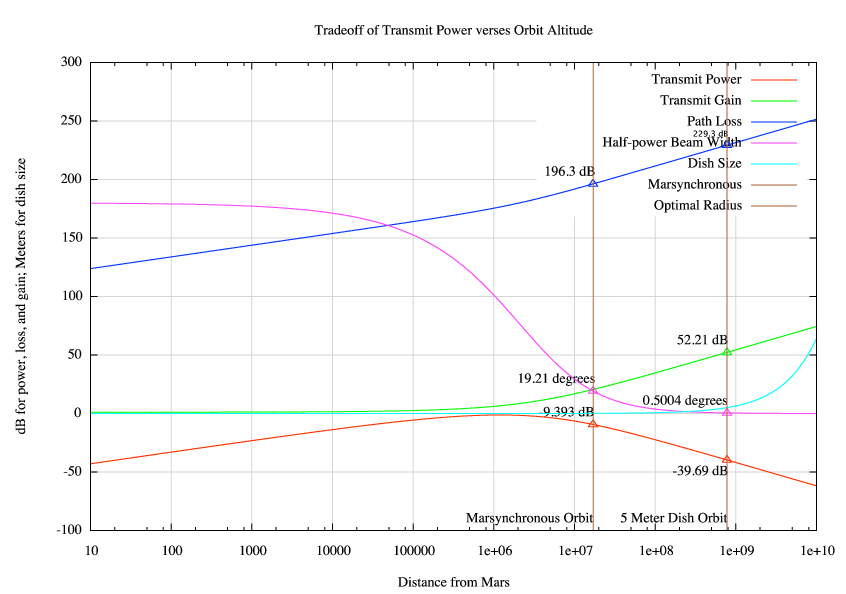
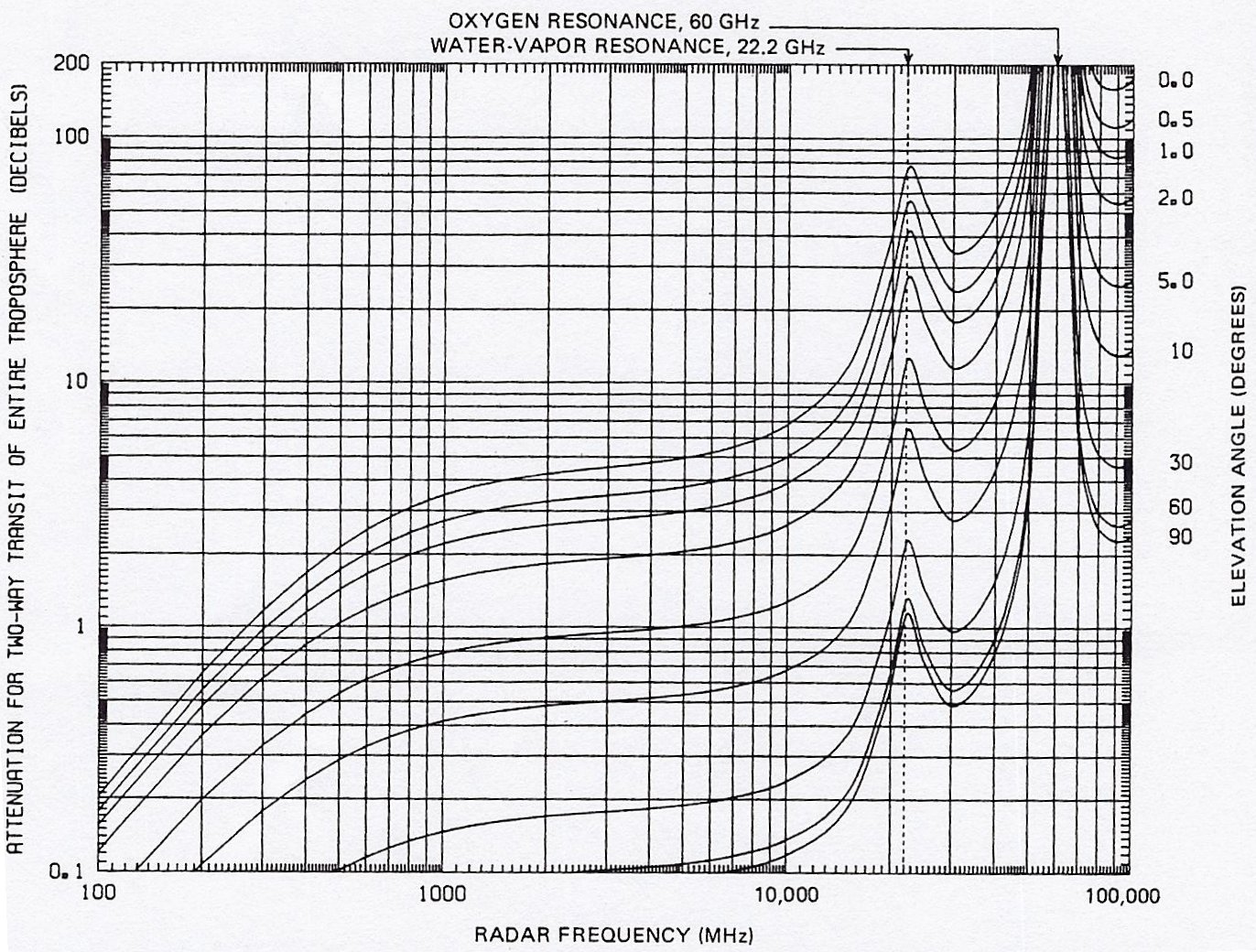
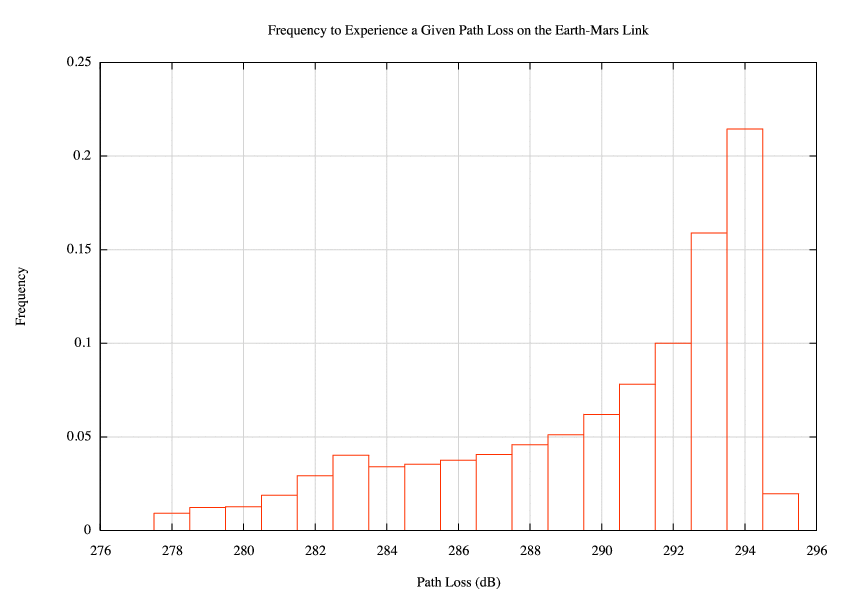
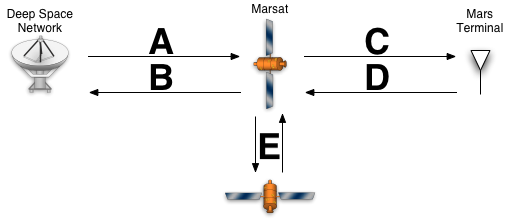
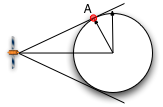 The link loss plotted on the chart, is the HPBW point denoted by A in the figure to the right. Also, 3 dB was added to the transmit power to ensure that terminals at point A would receive at least 0 dB of C/N. This is beyond a worst case however, because a terminal at point A, would have a closer satellite to correspond with.
The link loss plotted on the chart, is the HPBW point denoted by A in the figure to the right. Also, 3 dB was added to the transmit power to ensure that terminals at point A would receive at least 0 dB of C/N. This is beyond a worst case however, because a terminal at point A, would have a closer satellite to correspond with.
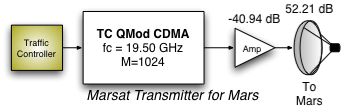
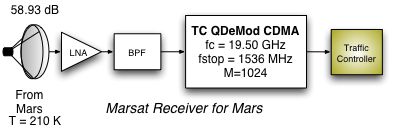
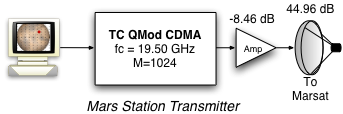
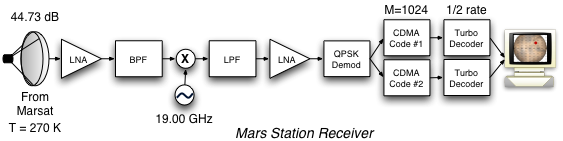
| Component | MARS to Mars | Mars to MARS |
|---|---|---|
| fc (GHz) | 19.00 | 19.50 |
| λ (m) | 0.015779 | 0.015374 |
| D (m) | 5 | 1 |
| η | 0.75 | 0.75 |
| C/N (dB) | 0.0 | 0.0 |
| GT (dB) | 52.21 | 48.242 |
| GR (dB) | 48.242 | 52.21 |
| PL (dB) | 247.78 | 295.2610 |
| Tsys (dB) | 28 | 210 |
| B (MHz) | 3 | 3 |
| PN (dB) | -140.61 | -132.37 |
| PT (dB) | -36.69 | -28.45 |
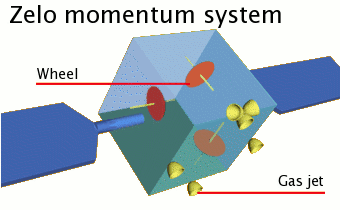 The MARS satellites will use the Zelo momentum system to perform orbital corrections. This system uses momentum wheels and gas jets to correct the motion and speed of the satellites. Accurate adjustments of our orbits becomes crutial when using narrow-beam lasers for inter-satellite communication.
The MARS satellites will use the Zelo momentum system to perform orbital corrections. This system uses momentum wheels and gas jets to correct the motion and speed of the satellites. Accurate adjustments of our orbits becomes crutial when using narrow-beam lasers for inter-satellite communication.
| Item | Count | Cost | Total (Millions) |
|---|---|---|---|
| Satellite | 3 | $200 | $600.00 |
| MarSat-Earth | 65.0115 Watts x 3 Sats | $1/Watt | $195.03 |
| MarSat-MarSat | 1 Watt x 6 Lasers | $1/Watt | $6.00 |
| MarSat-Mars | 0.00010740 x 3 Sats | $1/Watt | $0.00 |
| Polar Antennas | 2 Antennas | $100/Antenna | $200.00 |
| Total | $1001.00 |
| Module | Part # | Features | Cost |
|---|---|---|---|
| Turbo Code | ComBlock COM-7001 Turbo-Code Error Correction Demodulator |
Rate 0.25 to 0.97 Block Length: 64 bits to 4K bits |
$375 |
| Low Noise Amplifier | Northrop Grumman ALH403 |
27dB gain 61K Noise Temp @ 500MHz |
|
| Bandpass Filter | Wenzel Electronics Low Noise Bandpass Filter | Noise Temp: 36.214 @ 500 MHz | $44 |
| Local Oscillator | Epson EG-2121CA |
Low Jitter, High-frequency oscillator Accuracy: 50 ppm |
$54 |
| PN Code / BPSK Demodulator | COM-1011 Direct Sequence Spread-Spectrum Demodulator |
Built in BPSK/QPSK demodulator Code Searching & Receiver Lock |
$295 |
| Dish Antenna | Harris Satellites Dish Antenna | 4m diameter dish 50.2534 dBi gain @ 8.425 GhZ |
G = 6.67300E-11;
k = 1.3806503E-23;
AU = 149597870691;
c = 299792458;
DAY = 24*60*60;
mars_mass = 6.4185E23;
mars_rotation = 1.025957*DAY;
mmo = ( ( sqrt( G * mars_mass ) * mars_rotation ) / ( 2 * pi ) )^(2/3);
ff = 19E9;
rr = logspace( 1, 10, 3000 );
ll = 3E8./ff;
Pr = -129.36; %this is set to the noise power to make the C/N = 0
mr = 3402E3; % radius of mars
mu = 42828E9; % the GMp product
v = sqrt(mu./(rr+mr)); % the velocity of the satellite at altitude rr
eff = 0.75; % antenna efficiency
% I always wanted to use the half-power band width that would provide me the
% most surface of the planet. In section 3.4, there's an illustration of the
% satellite setting its HPBW at the tangent of the planent (point A).
% this equation finds that angle and multiplies it by 2 to get the HPBW
hpbwr = 2*asin(mr./(rr+mr)); % HPBW in radians
hpbwd = rad2deg(hpbwr); % HPBW in degrees
% this is the worst case doppler shift (actually beyond worst case)
dop = (1./ll).*(v.*sin(hpbwr./2) - (2*pi*mr/mars_rotation));
% gain of the transmitter based on the HPBW
Gt = lin2db(55517*eff ./ (hpbwd.^2));
% gain of the receiver based on the frequency
Gr = lin2db(eff*pi^2 ./ ll.^2);
% the diameter of the transmitting antenna
D = 75*ll./hpbwd;
% the height of the polar antenna
A = (rr+mr).*tan(hpbwr/2) - mr;
% index of the optimal value (since I can use a dish larger than 5 meters)
i = max(find(D<5));
% index of the marsynchronous orbit
n = max(find(rr<(mmo-mr)));
% the furthest point of communication at the HPBW line (worse than worse case)
rh = rr./cos(hpbwr/2);
% Path loss based on WtWCS
PL = 2*lin2db(4*pi ./ ll) + 2*lin2db( rh );
% HPBW is 3 dB down, so I need to give them 3 dB more power
HP = 3;
% Required transmit power
Pt = Pr - Gt - Gt - Gr + PL + HP;
text;
semilogx( rr, dop/1E6, '-;Doppler Shift;', \
[mmo-mr-1E-6 mmo-mr+1E-6], [-0.1 0.2], '-k;Marsynchronous;', \
[rr(i)-1E-6 rr(i)+1E-6], [-0.1 0.2], '-k;Optimal Radius;' );
xlabel( 'Distance from Mars' );
ylabel( 'Frequency Shift (MHz)' );
title( 'Doppler Shift vs. Orbit Elevation' );
text;
semilogx( rr, Pt, '-;Transmit Power;', rr, Gt, '-;Transmit Gain;', \
rr, PL, '-;Path Loss;', rr, hpbwd, '-;Half-power Beam Width;', \
rr, D, '-;Dish Size;', \
rr(n), PL(n), '*b;;', \
rr(n), hpbwd(n), '*m;;', \
rr(n), Pt(n), '*r;;', \
rr(i), PL(i), '*b;;', \
rr(i), hpbwd(i), '*m;;', \
rr(i), Pt(i), '*r;;', \
rr(i), Gt(i), '*g;;', \
[mmo-mr-1E-6 mmo-mr+1E-6], [-100 300], '-k;Marsynchronous;', \
[rr(i)-1E-6 rr(i)+1E-6], [-100 300], '-k;Optimal Radius;' );
text( rr(n), -90, 'Marsynchronous Orbit', 'HorizontalAlignment', 'right' );
text( rr(i), -90, '5 Meter Dish Orbit', 'HorizontalAlignment', 'right' );
text( rr(n), PL(n)+10, strcat(num2str(PL(n)),' dB'), 'HorizontalAlignment', 'right' );
text( rr(n), Pt(n)+10, strcat(num2str(Pt(n)),' dB'), 'HorizontalAlignment', 'right' );
text( rr(n), hpbwd(n)+10, strcat(num2str(hpbwd(n)),' degrees'), 'HorizontalAlignment', 'right' );
text( rr(i), PL(i)+10, strcat(num2str(PL(i)),' dB'), 'HorizontalAlignment', 'right', 'FontSize', 8 );
text( rr(i), Pt(i)-10, strcat(num2str(Pt(i)),' dB'), 'HorizontalAlignment', 'right' );
text( rr(i), hpbwd(i)+10, strcat(num2str(hpbwd(i)),' degrees'), 'HorizontalAlignment', 'right' );
text( rr(i), Gt(i)+10, strcat(num2str(Gt(i)),' dB'), 'HorizontalAlignment', 'right' );
xlabel( 'Distance from Mars' );
ylabel( 'dB for power, loss, and gain; Meters for dish size' );
title('Tradeoff of Transmit Power verses Orbit Altitude');
bpsec=75E6;
rate=1/2;
fc=34.45E9;
bpsym=2;
allocated = 500E6;
doppler = 2E6;
alpha = 0.1;
f0 = bpsec/(rate * bpsym);
N = 2^9;
t1 = -20/f0;
t2 = -t1;
t = linspace(t1,t2,64);
f = (-N/2:N/2 - 1)/(t2-t1);
x = (sin(2*pi*f0*t)./(2*pi*f0*t)).*(cos(2*pi*alpha*t*f0)./(1-(4*alpha*f0*t).^2)); % raised cosine pulse
axis;
plot(t,x,'-;;');
title('Raised Cosine with a Rolloff Factor of 0.3');
xlabel('time (s)');
ylabel('Amplitude');
X = fft(x,N);
XX = abs(fftshift(X))*(t2-t1)/N;
XX_new = 20*log10(XX/max(XX));
axis( [ -1000 1000 -100 0.2 ] );
plot(f/1E6,XX_new,'-;;'), grid on
xlabel('Frequency (MHz)'), ylabel('Power (dB)');
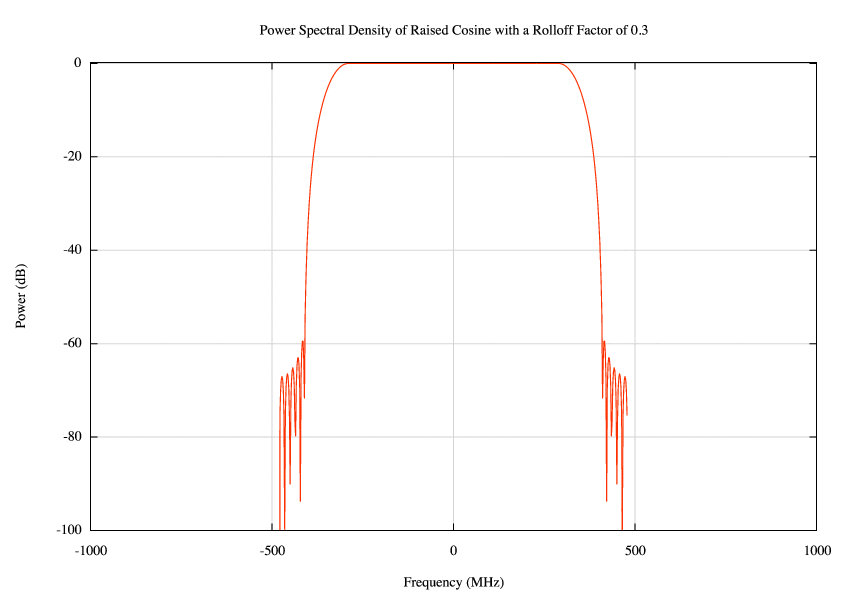
title('Power Spectral Density of Raised Cosine with a Rolloff Factor of 0.3');
package MarsSim::Constants; require Exporter; @ISA = qw(Exporter); @EXPORT = qw(M KM AU KG PI DEGREE K SEC MIN HOUR DAY YEAR G LIGHT_YEAR JULIAN_YEAR Hz kHz MHz GHz THz c pi k); # time in seconds # temp in kelvin # mass in kilograms # angles in radians # length in meters use constant M => 1; use constant KM => 1E3; use constant AU => 149597870.691*KM; use constant KG => 1; use constant PI => 3.14159; use constant DEGREE => 180/PI; use constant K => 1; use constant SEC => 1; use constant MIN => 60; use constant HOUR => 60*MIN; use constant DAY => 24*HOUR; use constant YEAR => 365.25641*DAY; use constant G => 6.67300E-11; # m3 kg-1 s-2 use constant LIGHT_YEAR => 9.4605284E15*M; use constant JULIAN_YEAR => 365.25*DAY; use constant Hz => 1; use constant kHz => 1E3; use constant MHz => 1E6; use constant GHz => 1E9; use constant THz => 1E12; use constant c => 299792458; use constant pi => 3.14159265; use constant k => 1.3806503E-23; # m2 kg s-2 K-1 (Boltzmann's Constant) 1;
package MarsSim::Antenna;
use Exporter;
use MarsSim::Constants;
use MarsSim::Misc;
@EXPORT = qw(new);
sub new {
my( $class, %options ) = @_;
die "Cannot create an antenna without a lambda or frequency\n"
unless( defined( $options{lambda} ) || defined( $options{frequency} ) );
die "Cannot calculate gain\n"
unless( defined( $options{gain} ) || defined( $options{hpbw} ) || defined( $options{area} ) || defined( $options{diameter} ) );
$options{lambda} = c / $options{frequency} unless defined $options{lambda};
$options{efficiency} = 1 unless defined $options{efficiency};
if( defined( $options{diameter} ) ) {
$options{area} = diameter2area( $options{diameter} );
$options{gain} = area2gain( $options{area}, $options{efficiency}, $options{lambda} );
$options{hpbw} = diameter2hpbw($options{diameter}, $options{lambda});#gain2hpbw( $options{gain} );
} elsif( defined( $options{hpbw} ) ) {
$options{gain} = hpbw2gain( $options{hpbw} );
$options{area} = gain2area( $options{gain}, $options{efficiency}, $options{lambda} );
$options{diameter} = area2diameter( $options{area} );
} else {
$options{area} = gain2area( $options{gain}, $options{efficiency}, $options{lambda} );
$options{diameter} = area2diameter( $options{area} );
$options{hpbw} = gain2hpbw( $options{gain} );
}
$options{temp} = 270*K unless defined $options{temp};
$options{bandwidth} = 1 unless defined $options{bandwidth};
bless \%options, $class;
return \%options;
}
sub gain {
my( $self, $lambda ) = @_;
return( $self->{efficiency}*4*pi*$self->{area} / ($lambda**2) );
}
sub linkloss {
my( $self, $distance, $dbflag ) = @_;
my $ll = ( 4 * pi * $distance ) / $self->{lambda};
return( ($dbflag) ? 2*lin2db($ll) : $ll );
}
sub noise {
my( $self, $dbflag ) = @_;
my $n = k*$self->{tempature}*$self->{bandwidth};
return( ($dbflag) ? lin2db($n) : $n );
}
sub hpbw2gain { return( 33000 / (shift()**2) ); }
sub gain2hpbw { return( sqrt(33000 / shift()) )}
sub diameter2area { return( pi*((shift()/2)**2) ); }
sub area2diameter { return( 2*sqrt(shift()/pi) ); }
sub area2gain {
my( $area, $eff, $lambda ) = @_;
return( $eff*4*pi*$area / ($lambda**2) );
}
sub gain2area {
my( $gain, $eff, $lambda ) = @_;
return( $gain * ($lambda**2) / ($eff * 4 * pi) );
}
sub diameter2hpbw {
my( $dia, $lambda ) = @_;
return( 75*$lambda / $dia );
}
1;
package MarsSim::Planet;
use MarsSim::Constants;
sub new {
my( $class, %o ) = @_;
bless \%o, $class;
return \%o;
}
sub geosynch_radius {
my( $self ) = @_;
return( ( ( sqrt( G * $self->{mass} ) * $self->{rotation_period} ) / ( 2 * pi ) )**(2/3) );
}
1;
package MarsSim::Star;
sub new {
my( $class, %o ) = @_;
bless \%o, $class;
return \%o;
}
1;
#!/usr/bin/perl -w
use strict;
use MarsSim::Antenna;
use MarsSim::Constants;
use MarsSim::Misc;
use MarsSim::Star;
use MarsSim::Planet;
use Data::Dumper;
my $sun = new MarsSim::Star(
galactic_radius => 26000*LIGHT_YEAR,
galactic_period => 2.26E8*JULIAN_YEAR,
diameter => 1.392E6*KM,
mass => 1.9891E30*KG,
rotation_period => 25.3800*DAY,
);
my $mars = new MarsSim::Planet(
semimajor => 1.52366231*AU,
eccentricity => 0.09341233,
perihelion => 1.38133346*AU,
orbit_period => 686.9600*DAY,
inclination => 5.65*DEGREE,
eqatorial_diameter => 6804.9*KM,
polar_diameter => 6754.8*KM,
mass => 6.4185E23*KG,
rotation_period => 1.025957*DAY,
axial_tilt => 25.19*DEGREE,
temp_min => 133*K,
temp_mean => 210*K,
temp_max => 293*K,
orbits => $sun,
);
my $earth = new MarsSim::Planet(
semimajor => 152097701*KM,
eccentricity => 0.016710150,
perihelion => 147098074*KM,
orbit_period => 365.25641*DAY,
inclination => 7.25*DEGREE,
eqatorial_diameter => 12756.270*KM,
polar_diameter => 12713.500*KM,
mass => 5.9736E24*KG,
rotation_period => 23.934*HOUR,
axial_tilt => 23.439281*DEGREE,
temp_min => 185*K,
temp_mean => 287*K,
temp_max => 331*K,
orbits => $sun,
);
#my $marsat = new MarsSim::Satellite(
# orbits => $mars,
# eccentricity => 0,
# orbit_radius => $mars->geosynch_orbit(),
#);
my $dsn = new MarsSim::Antenna(
power => 500E3,
diameter => 34,
frequency => 34.45*GHz,
bandwidth => 150*MHz,
efficiency => 0.94,
tempature => 270*K,
location => $earth,
);
my $marsat = new MarsSim::Antenna(
power => db2lin(18.2340),
diameter => 5,
frequency => 32.05*GHz,
bandwidth => 150*MHz,
efficiency => 0.75,
tempature => 28*K,
);
my $marsat2 = new MarsSim::Antenna(
power => db2lin(-40.94),
diameter => 5,
#hpbw => 19,
frequency => 19*GHz,
bandwidth => 3*MHz,
efficiency => 0.75,
tempature => 28*K,
);
my $station = new MarsSim::Antenna(
power => db2lin(-40),
diameter => 1,
frequency => 19.5*GHz,
bandwidth => 3*MHz,
efficiency => 0.75,
tempature => 210*K,
);
my $r = 7.7559e+08;
print( "===== Mars Satellite to Earth =====\n" );
snr2( $marsat, $dsn, 401.3E9, 0 );
print( "===== Earth to Mars Satellite =====\n" );
snr2( $dsn, $marsat, 401.3E9, 0 );
print( "===== Mars Station to Mars Satellite =====\n" );
snr2( $station, $marsat2, $r, 0 );
print( "===== Mars Satellite to Mars Station =====\n" );
snr2( $marsat2, $station, $r, 0 );
sub snr {
my($send, $recv, $dist)=@_;
my $pt = $send->{power};
printf( "Cost per satellite: \$%0.4f million dollars\n", $pt + 200 );
my $e1 = $send->{efficiency};
my $e2 = $recv->{efficiency};
#my $fc = 8.43*GHz; my $bw = 60*MHz;
my $fc = $send->{frequency};
my $bw = $send->{bandwidth};
my $d1 = $send->{diameter};
my $d2 = $recv->{diameter};
my $d = $dist;
my $t = $send->{tempature};
my $l = c / $fc;
print( "SNR = Pt + Gt + Gr - PL - Pn\n" );
my $Pt = lin2db( $send->{power} );
my $Gt = lin2db( $e1 * ((pi*$d1)**2) / ($l**2) );
my $Gr = lin2db( $e2 * ((pi*$d2)**2) / ($l**2) );
my $PL = 2*lin2db( $fc*4*pi*$d/c );
my $Pn = lin2db( k*$t*$bw );
printf( "Pt = %0.4f\n", $Pt );
printf( "Gt = %0.4f\n", $Gt );
printf( "Gr = %0.4f\n", $Gr );
printf( "PL = %0.4f\n", $PL );
printf( "Pn = %0.4f\n", $Pn );
my $snr = $Pt + $Gt + $Gr - $PL - $Pn;
printf( "SNR = %0.4f\n", $snr );
}
sub snr2 {
my($send, $recv, $dist, $snr)=@_;
my $pt = $send->{power};
my $e1 = $send->{efficiency};
my $e2 = $recv->{efficiency};
#my $fc = 8.43*GHz; my $bw = 60*MHz;
my $fc = $send->{frequency};
my $bw = $send->{bandwidth};
my $d1 = $send->{diameter};
my $d2 = $recv->{diameter};
my $d = $dist;
my $t = $send->{tempature};
my $l = c / $fc;
print( "Pt = SNR - Gt - Gr + PL + Pn\n" );
my $Gt = lin2db( $e1 * ((pi*$d1)**2) / ($l**2) );
my $Gr = lin2db( $e2 * ((pi*$d2)**2) / ($l**2) );
my $PL = 2*lin2db( $fc*4*pi*$d/c );
my $Pn = lin2db( k*$t*$bw );
printf( "SNR = %0.4f\n", $snr );
printf( "Gt = %0.4f\n", $Gt );
printf( "Gr = %0.4f\n", $Gr );
printf( "PL = %0.4f\n", $PL );
printf( "Pn = %0.4f\n", $Pn );
my $Pt = $snr - $Gt - $Gr + $PL + $Pn;
printf( "Pt = %0.4f\n", $Pt );
printf( "Cost per satellite: \$%0.4f million dollars\n", db2lin($Pt) + 200 );
}
| Property | Mars | Earth | Ratio (Mars/Earth) |
|---|---|---|---|
| Mass (1024 kg) | 0.64185 | 5.9736 | 0.107 |
| Volume (1010 km3) | 16.318 | 108.321 | 0.151 |
| Equatorial radius (km) | 3397 | 6378.1 | 0.533 |
| Polar radius (km) | 3375 | 6356.8 | 0.531 |
| Volumetric mean radius (km) | 3390 | 6371.0 | 0.532 |
| Core radius (km) | 1700 | 3485 | 0.488 |
| Ellipticity (Flattening) | 0.00648 | 0.00335 | 1.93 |
| Mean density (kg/m3) | 3933 | 5515 | 0.713 |
| Surface gravity (m/s2) | 3.71 | 9.80 | 0.379 |
| Surface acceleration (m/s2) | 3.69 | 9.78 | 0.377 |
| Escape velocity (km/s) | 5.03 | 11.19 | 0.450 |
| GM (x 106 km3/s2) | 0.04283 | 0.3986 | 0.107 |
| Bond albedo | 0.250 | 0.306 | 0.817 |
| Visual geometric albedo | 0.150 | 0.367 | 0.409 |
| Visual magnitude V(1,0) | -1.52 | -3.86 | - |
| Solar irradiance (W/m2) | 589.2 | 1367.6 | 0.431 |
| Black-body temperature (K) | 210.1 | 254.3 | 0.826 |
| Topographic range (km) | 30 | 20 | 1.500 |
| Moment of inertia (I/MR2) | 0.366 | 0.3308 | 1.106 |
| J2 (x 10-6) | 1960.45 | 1082.63 | 1.811 |
| Number of natural satellites | 2 | 1 | |
| Planetary ring system | No | No |
| Property | Mars | Earth | Ratio (Mars/Earth) |
|---|---|---|---|
| Semimajor axis (106 km) | 227.92 | 149.60 | 1.524 |
| Sidereal orbit period (days) | 686.980 | 365.256 | 1.881 |
| Tropical orbit period (days) | 686.973 | 365.242 | 1.881 |
| Perihelion (106 km) | 206.62 | 147.09 | 1.405 |
| Aphelion (106 km) | 249.23 | 152.10 | 1.639 |
| Synodic period (days) | 779.94 | - | - |
| Mean orbital velocity (km/s) | 24.13 | 29.78 | 0.810 |
| Max. orbital velocity (km/s) | 26.50 | 30.29 | 0.875 |
| Min. orbital velocity (km/s) | 21.97 | 29.29 | 0.750 |
| Orbit inclination (deg) | 1.850 | 0.000 | - |
| Orbit eccentricity | 0.0935 | 0.0167 | 5.599 |
| Sidereal rotation period (hrs) | 24.6229 | 23.9345 | 1.029 |
| Length of day (hrs) | 24.6597 | 24.0000 | 1.027 |
| Obliquity to orbit (deg) | 25.19 | 23.45 | 1.074 |
| Property | Phobos | Deimos |
|---|---|---|
| Semi-major axis* (km) | 9378 | 23459 |
| Sidereal orbit period (days) | 0.31891 | 1.26244 |
| Sidereal rotation period (days) | 0.31891 | 1.26244 |
| Orbital inclination (deg) | 1.08 | 1.79 |
| Orbital eccentricity | 0.0151 | 0.0005 |
| Major axis radius (km) | 13.4 | 7.5 |
| Median axis radius (km) | 11.2 | 6.1 |
| Minor axis radius (km) | 9.2 | 5.2 |
| Mass (1015 kg) | 10.6 | 2.4 |
| Mean density (kg/m3) | 1900 | 1750 |
| Geometric albedo | 0.07 | 0.08 |
| Visual magnitude V(1,0) | +11.8 | +12.89 |
| Apparent visual magnitude (V0) | 11.3 | 12.40 |
| Surface pressure | 6.36 mb at mean radius (variable from 4.0 to 8.7 mb depending on season) [6.9 mb to 9 mb (Viking 1 Lander site)] |
|---|---|
| Surface density | ~0.020 kg/m3 |
| Scale height | 11.1 km |
| Total mass of atmosphere | ~2.5 x 1016 kg |
| Average temperature | ~210 K (-63 C) |
| Diurnal temperature range | 184 K to 242 K (-89 to -31 C) (Viking 1 Lander site) |
| Wind speeds | 2-7 m/s (summer), 5-10 m/s (fall), 17-30 m/s (dust storm) (Viking Lander sites) |
| Mean molecular weight | 43.34 g/mole |
| Atmospheric composition (by volume) | |
| Major | Carbon Dioxide (CO2) - 95.32% ; Nitrogen (N2) - 2.7% ; Argon (Ar) - 1.6%; Oxygen (O2) - 0.13%; Carbon Monoxide (CO) - 0.08% |
| Minor (ppm) | Water (H2O) - 210; Nitrogen Oxide (NO) - 100; Neon (Ne) - 2.5; Hydrogen-Deuterium-Oxygen (HDO) - 0.85; Krypton (Kr) - 0.3; Xenon (Xe) - 0.08 |