Given the signal from an EPIRB, its position must be calculated as described in the Project Statement.

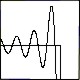
Approach

To get the latitude coordinate, we found the minimum and maximum frequency.  The average of these two gave the center frequency, which is most likely the actually frequency the EPIRB is transmitting.  Using the intercept time from the given data and the angular velocity of the orbiting satellite, we were able to estimate the latitude.  

Finding the longitude required taking a derivative of the frequency data, which had some measurement error.  A simple digital low pass filter was used to smooth the frequency data to provide a more accurate estimate of the derivative, found using the 'diff' function.  The point in the frequency data where the derivative was the greatest corresponds to the point where the satellite is at the same latitude as the EPIRB.  Using this derivative and the Doppler shift formula, we set up a difference equation to determine the change in angle between the EPIRB and the satellite over one second.  Using this angle information and the velocity of the satellite, we solved for the distance between the satellite and the EPIRB at the point in which their latitudes are the same.  Some simple trigonometry gave a longitude estimate.

See the elaborate comments in the Matlab code for more details of our method. (sarsat.m, mylpf.m)

Results

The EPIRB receiver is at a location of 25.4516583° Lat and -78.6742404° Lon.  This is close to the Bimini island in the Bahamas.

Comments

Taking a more accurate numerical derivative should increase the accuracy of the results.

The SARSAT system is accurate to about 1 km.  Our computational method probably does not achieve this accuracy for the longitude coordinate.

An unknown frequency can be found using a FFT algorithm.