A Channel Model Approach

In order to determine the maximum switching rate of the receiver, the wireless channel was first modeled with an azimuth spectrum.  An azimuth spectrum showed the distribution of electromagnetic waves incident upon a given location as a function of angle.  The Shinkansen train travels through both rural and urban areas, so there were two main azimuth spectra to be dealt with.  For rural locations, the multipath problem was small due to fewer objects in the environment.  Therefore, the power of azimuth spectrum would be concentrated around the angle pointing toward the nearest base station.   For more urban locale, the multipath problem was much more significant due to numerous obstructions in the environment.  Therefore, urban locations would have an azimuth spectrum with power nearly evenly distributed through all angles, though slightly strong in the direction of the base station.  To properly model the azimuth distributions, the following function was used:

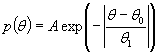                                                          (Eq. 1)

The value theta0 is the direction of the base station.  The value theta1 controls the spread of the distribution.  A value of 120 degrees was used to represent the spread of the azimuth spectrum in urban areas, and a value of 3 degrees was used for rural areas.  Because the direction of the train relative to the base station played a significant role in the effectiveness of the dual monopole antennas, the small-scale fading had to be analyzed for when the train was moving toward as well as traverse to the base station.  This resulted in a total of four cases for which to model the small-scale fading as shown in the figure below.

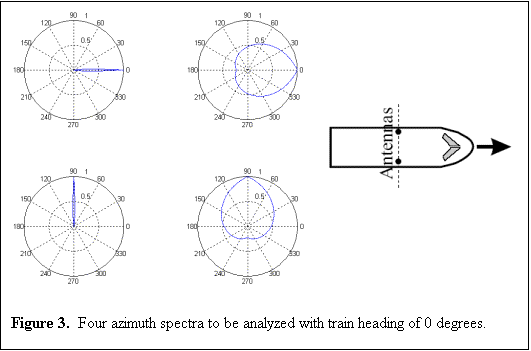The continuous azimuth spectrum may be simulated by using a discrete number of plane waves with random phase offsets.  The total z-component of these fields would then be given by the following equation:

        (Eq. 2)

                                                           (Eq. 3)

The variable U_n was a uniformly distributed random variable from 0 to 1 and controlled the random phase offset of a given plane wave.

Given the azimuth spectrum of the multipath, it is possible to calculate various shape factors describing the azimuth spectrum and thereby determine the level crossing rate and fade duration.  To find the shape factors, one must first calculate the Fourier coefficients of the spectrum:

                                                    (Eq. 4)

From here, one may calculate the three shape factors:

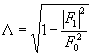                                                                          (Eq. 5)

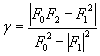                                                                        (Eq. 6)

                                                           (Eq. 7)

The variable represents the angular spread of the azimuth spectrum.  The variable  represents the angular constriction of the spectrum, which is a measure of how much the multipath is concentrated about two azimuthal directions.  The variable represents the direction of maximum fading.

The level-crossing rate, , and the average fade duration, , are then given by the following equations:

                  (Eq. 8)

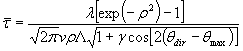                                     (Eq. 9)

 The value  is the normalized threshold, and  is the direction of travel with velocity .

For the Laplacian azimuth spectrum, the equation for the Fourier coefficients becomes the following:

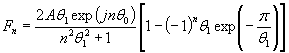                        (Eq. 10)

where  and  are in radians.  From here, the shape factors may be calculated.  The values are presented in Table 1.

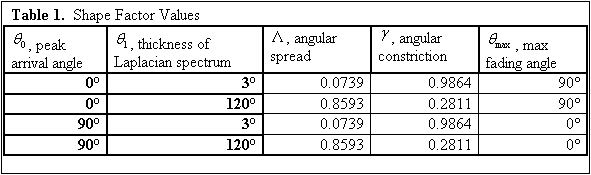Greater angular spread will naturally lead to greater small-scale fading, so the antennas on the train will experience the greatest small-scale fading when  is 120°.  The train’s heading is 0° degrees, and the case when =90° and= 120° causes maximum fading at an angle of 0°.  Thus, the =90°,  = 120° case will represent the worst-case scenario for small-scale fading as experienced by the high-speed bullet train.  This is the case that will be used in determining the maximum sampling and switching rate of the receiver.

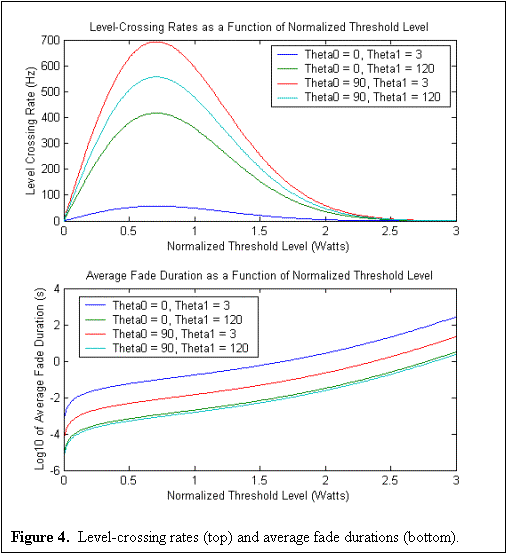
Finally, for completeness, plots of the level-crossing and average fade duration as a function of  are presented in Figure 4.