Determining the Maximum Necessary Switching Rate

The train was assumed to be heading in the x-direction at a velocity v_train = 260 km/h.  For this scenario, the dual monopole antennas would then be separated by 2 meters in the y-direction.  To model the total field along the antennas’ paths of travel, the field was evaluated at the points (x, 0) and (x, -2).  When this data was plotted, it showed the small-scale fading experienced at each of the two receiver antennas.  By dividing the independent variable x by the velocity of the train, the small-scale fading as a function of time was determined.  The following figures show 100 ms of data for the four cases described earlier.

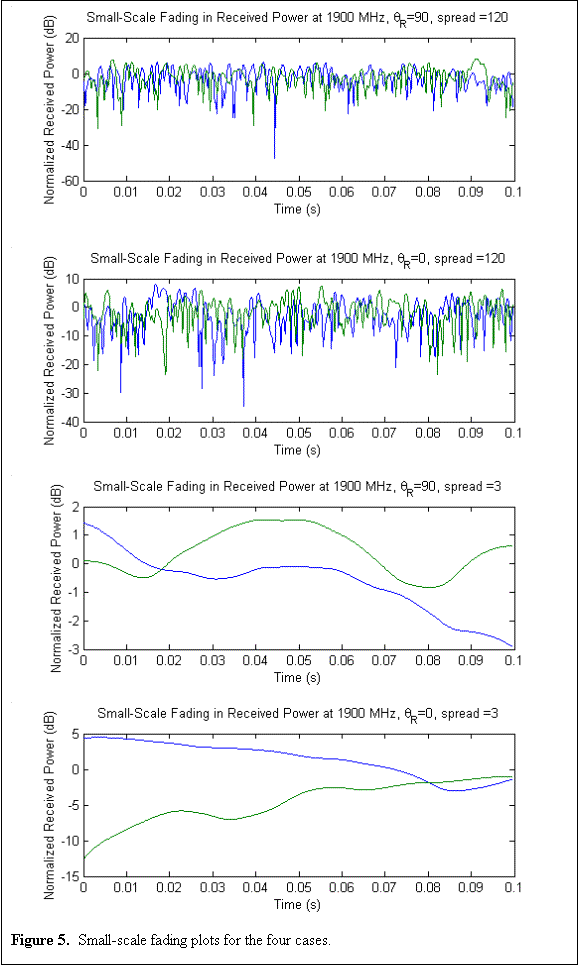To determine the level crossing rates based on this data, the average time intervals between crossings was determined.  A histogram of this data is shown in the figure below.  Note that the time between crossings is a random variable with a Rayleigh distribution.

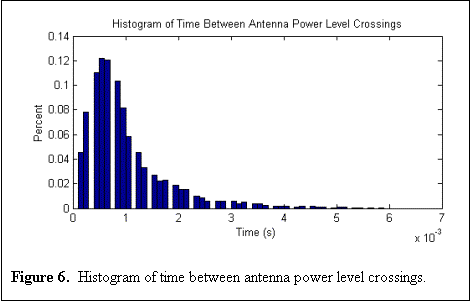By determining the mean and standard deviation of the data, an approximation for the actual Rayleigh probability density function  can be formed based on the equations given below:

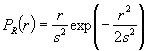                                                          (Eq. 11)

where  and is the mean of the distribution.

Converting the Rayleigh distribution from a function of time to a function of Hertz and then integrating results forms a very useful cumulative distribution function.  The new plot is a function of frequency and shows the percentage of power level crossing rates for the two antennas that are equal to or less than a given frequency rate.

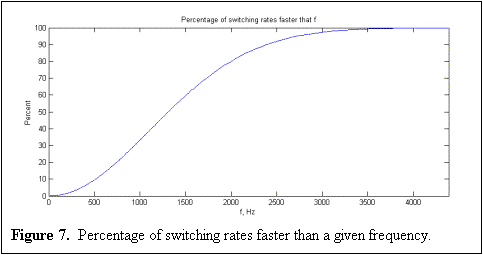According to this plot, it would require an infinite sampling rate to accurately monitor which antenna is receiving the strongest signal and switch to that antenna.  However, faster equipment costs more money, and NTT DoCoMo wants their diversity antenna system to be as cheap as possible.  Therefore, a compromise will have to be made between switching speed and the effectiveness of the selection diversity algorithm.  According to the plot, it appears that the best “bang for the buck” occurs somewhere between 2 and 2.5 kHz.  Therefore, the recommended sampling and switching rate of the receiver is 2.25 kHz, which is faster than about 85-90% of the power level crossing rates.  Additionally, because this analysis was performed for the worst-case scenario of small-scale fading where =90°,  = 120°, the sampling and switching rate will be more than adequate to handle the other three cases.