A great deal of consideration is made to try and directly incorporate the role of diffracted power into the total power received. The most promising and probably easiest method to implement is the Fresnel-Kirchoff solution to knife edge diffraction.
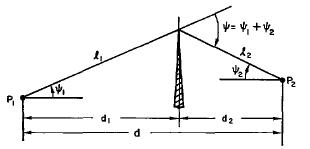
As seen in the figure, this method approximates any obstacle between the transmitter and receiver to be a single knife-edge. Furthermore, it assumes line of sight from both the receiver and transmitter to the tip of the knife-edge. From this approximation a diffraction power can be calculated. Remember that this linear equation must must be converted to logarithmic before it can be combined with the hybrid theoretical-empirical formula.
When checking the paths for line of sight or identifying the height and location of obstacles, several approximations are made. First, only the highest point between the receiver and the transmitter is considered to be an obstacle. Second, if there is more than one obstacle of the same height, then the obstacle closest to the transmitter is considered to be the knife edge.
Unfortunately, after calculating diffraction power for each of the sample regions it was determined to be less accurate than the previously discusses hybrid theoretical empirical model. This is due to the fact that the diffracted power calculation is solely theoretical and can only be made with significant approximations. With no empirical factors to correct for these overwhelming approximations, adding the diffracted power to the hybrid model simply compounds the error and results in a less accurate model. Therefore, the diffracted power is omitted from the calculation.
Diffraction still plays a large role in the model. Since there is no term in the calculation directly connecting diffraction, it becomes the dominant factor in shaping both the path loss exponent, n, and the correction factor c. See Technical Details.
Figure and Diffraction Power equation: [1]. See Sources.