2.0: Fundementals of Neptune
In this section the geometric and orbital problems of the project will be analyzed.
2.1: Physical Characteristics
Throughout this report there may be a need to use some basic physical quantities associated with Neptune. This section will be a reference for all the calculations that follow. Some values were obtained from the publication The planets Uranus, Neptune, and Pluto (1971), NASA SPACE VEHICLE DESIGN CRITERIA (Environment)
1
. The majority of information was obtained from Firefly's Astronomy Dictionary
2
.
One astronomical unit (AU):
The equatorial radius of Neptune
2
:
The polar radius of Neptune
2
:
Neptune's period of Rotation
2
:
Neptune's Gravitational Constant:
Neptune's Distance from Sun
2
:
A point of interest for this design is the radius of Neptune from its center to its 450 latitude line. since Neptune is elliptical in shape we can solve for this radius by writing the equation of an ellipse in an x, y Cartesian coordinate system. Once this ellipse is constructed the point where the x=y line intercepts the ellipse is used to find the desired radius at the 450 latitude line.
Neptune's radius at 450 latitude:
These two answers are the positive and negative results. The positive result will be taken and simplified. In the above calculation X45 is set to Y45. To find the 450 radius, R45, the Pythagorean formula is used, but since both distances are equal this is tantamount to multiplication by
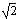in a 2 dimensional coordinate system.
To find geostationary orbit for Neptune Kepler's Third Law
3
is appropriate.
Section 2.1
and
section 1
have all the information we need:
The altitude of the orbit above Neptune is:
Several angles of interest are presented in the figure below. The first set of angles corresponds to a probe at the 450 latitude line that is just entering the atmosphere. The second set of angles corresponds to a probe that has descended 420km into the atmosphere.
All the information needed to calculate these angles is contained in the figure. First, Rt1 and Rt2 will be calculated using the law of cosines. The angles a1 and a2 can be obtained from the law of sines. Simple algebra will produce the other angles.
.
