Launch
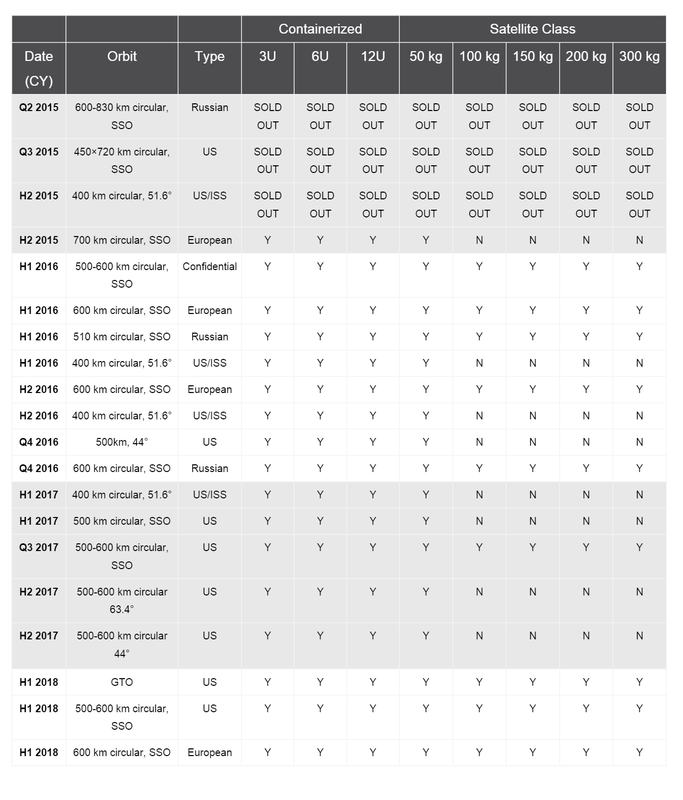
The MARCO POLO launch dates are estimated to take place no sooner than three years after project funding begins. There will be four separate launch dates to launch each set of cubesats into their respective four sun-synchronous low-Earth orbital planes. The launch will be contracted to SpaceFlight Industries. A table from their webpage detailing launch costs is provided below [1]. Highlighted is the launch cost of a low earth orbit (LEO) launch that would be capable of launching 22 MARCO POLO cubesats (a 99 kg payload) to sun-synchronous orbit.
SpaceFlight Industries operates via ride-sharing onto space missions with available space. Below are the near future launch dates provided by SpaceFlight [1]. The first MARCO POLO launch is estimated to be H2 of 2018, which is just out of the time-frame of this table. However, it is clear that SpaceFlight provides many sun-synchronous orbit (SSO) launch options to the 500 km altitude range per year.
The advantage of utilizing 4 launches to reach 4 different planes, in addition to spacing out the planes to avoid communication overlap, is that the less expensive 100 kg launches can be used. In order to launch all spacecraft at once, at 450 kg launch would be required, which costs more than 4x the 100 kg launches. The 21 or 22 spacecraft payload comes in just under the 100 kg launch limit, providing excellent payload utilization.
Constellation Deployment
Once on orbit, the satellites must be deployed and properly spaced in their orbit planes. If this were to be done using 86 individual launches to 86 separate orbits, the launch cost would be extraordinary! Alternatively, launching all 86 satellites at once would require large inclination changes, which is an expensive orbital maneuver [2]. This type of orbit change is not feasible using cubesat propulsion.
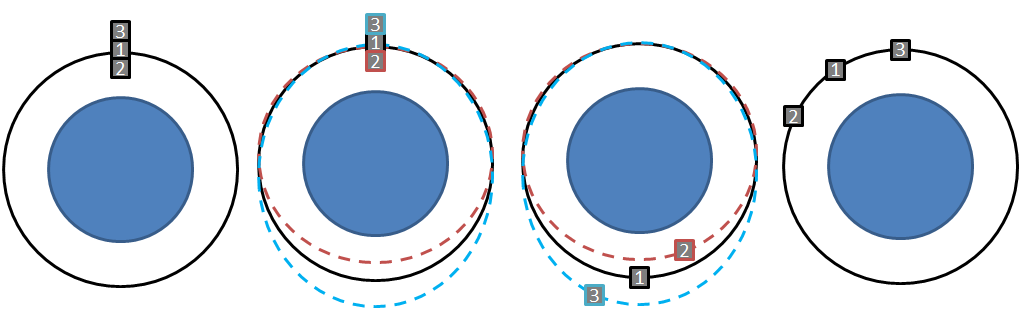
Instead, the preferred way of deploying a cubesat constellation is to release all the satellites for a certain plane at the same insertion point and have each satellite perform a small dual-burn semi-major axis change maneuver (commonly referred to as phasing) [3]. This works by slightly adjusting the period of the maneuvered satellite, making it speed up or slow down relative to the nominal orbit. At the point where the nominal and maneuvered orbits intersect, a second burn is performed to re-enter the nominal orbit, now at a different phase with respect to the neighboring satellites. This dual maneuver scheme requires very little velocity change, and thus can be accomplished using the selected propulsion unit. The constellation deployment scheme is further illustrated using the following figure.
Instead, the preferred way of deploying a cubesat constellation is to release all the satellites for a certain plane at the same insertion point and have each satellite perform a small dual-burn semi-major axis change maneuver (commonly referred to as phasing) [3]. This works by slightly adjusting the period of the maneuvered satellite, making it speed up or slow down relative to the nominal orbit. At the point where the nominal and maneuvered orbits intersect, a second burn is performed to re-enter the nominal orbit, now at a different phase with respect to the neighboring satellites. This dual maneuver scheme requires very little velocity change, and thus can be accomplished using the selected propulsion unit. The constellation deployment scheme is further illustrated using the following figure.
Initially, all three satellites begin in the same orbit. The 1st satellite does not maneuver, the 2nd satellite performs a perigee-lowering maneuver, while the 3rd satellite performs an apogee-raising maneuver. Now 2nd satellite has a shorter period and subsequently it is seen to be "ahead" of the 1st satellite after half an orbit. Conversely, the 3rd satellite has a longer period and lags behind. When the maneuvered satellites arrive back at the initial maneuver point (the intersection between the maneuvered and non-maneuvered trajectories) each satellite performs a burn equal to the original but in the opposite direction to re-join the nominal orbit.
This approach to orbit phasing can be applied to an arbitrarily large number of co-planar satellites. Additionally, the spacecraft can be allowed to drift for longer than one orbit period, increasing the phase change without increasing the propellant required, thus allowing large phase changes with low maneuvering requirements.
This approach to orbit phasing can be applied to an arbitrarily large number of co-planar satellites. Additionally, the spacecraft can be allowed to drift for longer than one orbit period, increasing the phase change without increasing the propellant required, thus allowing large phase changes with low maneuvering requirements.
References
[1] - SpaceFlight Industries - http://www.spaceflightindustries.com/schedule-pricing/
[2] - R. Bate, D. Mueller, J. White (1971) Fundamentals of Astrodynamics, Dover Publications, New York. ISBN 0486600610.
[3] - Bartkowicz, Orbit Phasing Maneuver - http://ccar.colorado.edu/asen5050/projects/projects_2012/bartkowicz/website/orbital_mechanics_4.html
[1] - SpaceFlight Industries - http://www.spaceflightindustries.com/schedule-pricing/
[2] - R. Bate, D. Mueller, J. White (1971) Fundamentals of Astrodynamics, Dover Publications, New York. ISBN 0486600610.
[3] - Bartkowicz, Orbit Phasing Maneuver - http://ccar.colorado.edu/asen5050/projects/projects_2012/bartkowicz/website/orbital_mechanics_4.html