Communication Systems
Overview
The Epsilon Eridani solar system is 10.5 light years away from Earth, which is 9.46e12 km.
This is a very long distance! The path loss for the entire link is given by:
Path Loss (dB) = 20*log10(4πrf/c) = 401.011 dB
(Where r = 9.46e15 m, f = 27 GHz, and c = 3e8 m/s)
This is obviously a very large amount of loss to overcome, and we found that a single satellite link over this distance was insufficient for transmitting data by itself. By using the link budget equation, we decided to use nine relay satellites to receive an adequate SNR at the Earth. Eight of these satellites span the distance between the Sun and Epsilon Eridani, and one of them orbits the Earth. The transmission from the orbiting relay will be sent to a station on Earth. Thus, each individual link between adjacent satellites will cover approximately 1.1502 light years. The relays will be identical to each other and launched sequentially so that they are equally spaced along the trajectory of the probe. For the purposes of this initial study, the radial velocity of Epsilon Eridani with respect to the Earth was neglected. Accounting for the radial velocity would complicate the requirement that the relays be equally spaced.
Once the initial probe satellite reaches the Epsilon Eridani system and acquires images it will begin transmission back to earth. The final relay probe closest to earth will transmit to another satellite orbiting the earth, which can then transmit the data down to the DSN earth station. Besides the fact that this is the shortest and simplest part of the link, earth-orbiting satellites will have significantly improved by the time the Space Busters probe is ready to transmit back images from the ex-solar system. By far the most challenging portion of the communication link will be transmitting from the Epsilon Eridani system back to our own solar system. It is important to remember that the transmission time will be approximately 10.5 years (the processing/regeneration time delay at each relay will be negligible compared to the total path distance travel time). So the future folks who inherit this project on the earth, after waiting centuries for the probe’s arrival at E. Eridani, will have to wait another decade before receiving the images taken!
Our frequency for transmission is 27 GHz, which falls in the Ka band. The choice of higher frequency produces higher antenna gain (very important for such a long distance link), as well as higher directionality. This also would produce a large Doppler shift (many GHz) if transmitting to a stationary receiver, since the velocity of the probes traveling to the exo-solar system will be very high. However, since all the relay satellites will be traveling in the same direction at similar speeds, the Doppler shift would not be a significant issue for most of the link. This frequency shift will have to be accounted for in the transmission between the transmitting probe (which will be orbiting E. Eridani) and the first relay satellite, and for the link between the last relay and the earth-orbiting satellite which acts as a downlink to the earth station receiver.
By using a Turbo Code (see section on coding for more detail), we can approach the Shannon Limit, where Eb/N0 = 1.5849 to achieve BER ≤ 10-6. Our chosen bit rate is very low, at 20 bits/sec, using BPSK modulation (where bandwidth=bit rate). This works since speed of transmission is not critical, but reliability is important for such a challenging long-distance link. This choice of data rate and modulation produces a required SNR of 2 dB, obtained by:
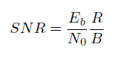
Where SNR is the required Signal to Noise Ration, B the bandwidth and R the bit rate. Thus,
SNR= (energy per bit * bits per second ) / (noise density * bandwidth).
The Shannon Limit here is 27.4021 bps, which is faster than our chosen bit rate, R<C.
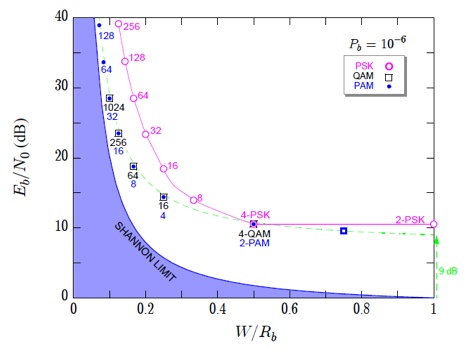
Shannon Limit and (uncoded) gap to capacity for different modulation formats and spectral efficiencies
BPSK Signal Constellation
Even with relays, the link budget will still be very demanding. We use a transmit power of 2kW (33 dBW). The antennas on each satellite will have 6.5 m radius, which produces a peak gain of nearly 71.5 dBi, assuming a parabolic dish antenna with efficiency of 0.9. In this way we can achieve a CNR of 2 dB, which allows us to meet our link budget.
Link Budget (dB): CNR = PT + GR + GT – 20*log10(4πrf/c) – PN = 2 dB
 |
 |
| (Voyager 2 High-gain antenna) | (New Horizons spacecraft showing antenna structure) |
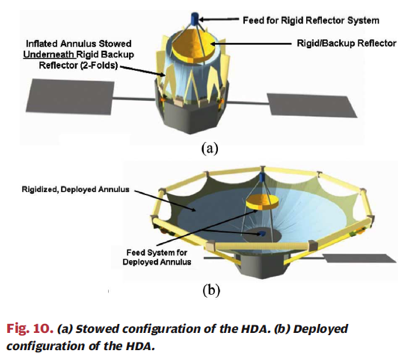
While previous deep-space missions have utilized high-gain antennas around 2-3 m in radius, we need a larger dish radius to achieve the gain necessary for this challenging mission. A newly developing technology is a hybrid deployable antenna (HDA). This type of design is known to make sense for an antenna side on the order of 10 m for future deep space missions, and offers better communication capability while minimizing risk of mission failure.
While inflatable/expandable antenna designs have had problems in the past, improvements in materials science have improved the robustness of this type of design. The HDA is a fully functioning antenna even in its non-expanded state, but can increase its diameter for high-gain transmission from deep space. This offers a level of redundancy and less risk, while offering the performance necessary for this challenging mission. Development of the antenna for Space Busters mission will take years of careful work, but should be able to meet the technical challenges of the communication system.
See Matlab code for all the detailed calculations for our communications link budget.