Communication Systems
Coding Scheme
I) Information Theory and Shannon Limit:
We know from information theory that the maximum capacity for a channel in bits per second is:
![]()
In our case let SNR be low, which is the case for Bà∞ that is assuming that the channel bandwidth is higher than the needed bandwidth.
Hence,
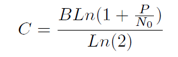
Becomes, with Ln(1+x) = x with x à0
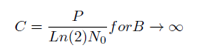
If R denotes the information data rate in bits/sec for Reliable Communication, from Shannon Theorem we have:
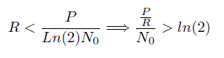
Where, P/R= Energy per unit Time/ Bits per Unit time = Eb , Energy per Bit. Then:
![]()
This is the fundamental limit that a reliable communication channel can achieve. Over the last few decades and the discovery of convolutional codes such as LDPC (Low Density Parity Check Codes) and Turbo Codes, we are getting close to this limit.
II/Coding Theory
1)Introduction
Turbo codes are the channel coding scheme used in wireless cellular networks as they are able to reach nearer to the Shannon limit. In this Section we introduce the basic definitions and notions in turbo codes, using different research articles; we were able to implement a 1/3 Turbo Encoder/Decoder. The decoding scheme relays on the BCJR algorithm, the Maximum Aposteriori Algorithm (MAP). For this purpose we have used Matlab to design this turbo code, (link to this part please refer to the download section)
It is important to notice that the second part of the code is just a proof of the good behavior of our implementation of the 1/3 Turbo Code. The reader can skip this part if he trusts the Space Busters. However, in order to study the behavior of our turbo code, we used an implementation of the EXIT charts, which enabled us to observe the evolution of information exchange between the two decoders after each iteration in the decoders.
2)Turbo Code Basic Concepts
We are going to introduce the basic concepts Turbo Codes. For a more detailed explanation please see the Turbo Code document. The Matlab code used for the simulation is also provided in the download section with the instructions to run it properly.
- Encoding
The turbo encoder uses convolutional encoder and feedback one of its encoded output to the input. We used a convolutional code with the Generator Matrix:[111; 101], to obtain an RCS block( Recursive Systematic Convolutional Block), included in the Turbo Encoder:
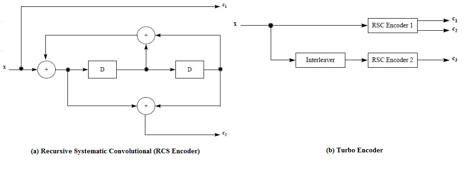
b) Decoding
In this section, we will describe the process of decoding using the BCJR algorithm.
Actually, the structure of a parallel turbo decoder is shown on the Figure below.
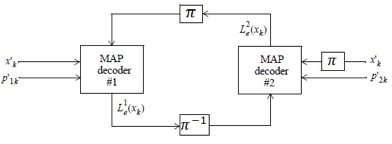
It consists of a pair of decoders which work cooperatively in order to refine and improve the estimate of the original bits.
The decoder are based on the BCJR algorithm, also called MAP (Maximum Aposteriori Probability) algorithm. The operation relies on soft decision information learned from each other. After initialization the soft decision of one decoder noted LE and named the extrinsic information is used to initialize the other decoder.
The decoded information is cycled around the loop until the soft decisions converge on stable set of values. In this case, we use the last extrinsic information issued from the first decoder to compute the estimate values of the message.
c) Implementation
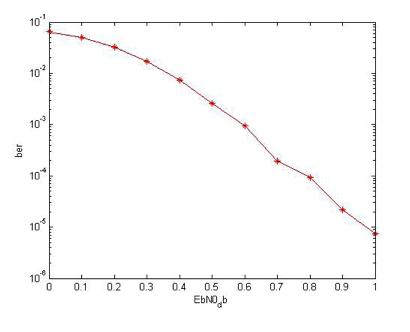
The designed Turbo Code will enable us to send the valuable data with very low Bit Error Rate (BER) 10^-6, with Eb/N0 of 2dB, this value has been used in the link Budget Part to estimate the longest Transmission Distance achieved and the number of relays needed in our Reliable Communication Channel.
We used our Matlab code with a size block of 10000 and 6 iterations. The number of iterations can be increased to 10, but for less power consumption in the uplink transmission, we used 6 iterations, which is already close to the needed BER.
In the Article “Near to Shannon Limit Error – Correcting Coding and Decoding : Turbo-Codes” [Ref], Claude Berrou designed a more complex Turbo Code, using a rate R=1/2 encoder with the Generator matrix G1=37, G2 =21. Equivalent to G=[100101;010101] , which is more complicated than our implementation and with a BER of 10^-5, he had a Eb/N0=0.7dB. Which, over the same conditions, is closer to the Shannon binary modulation with R=1/2
of a Eb/N0=0 dB !
This second complex coding scheme can be used if we provide enough processing capabilities and power in our relays. Remember that we have to take into account the Energy consumption because it is limited.
But, if we assume we are under these conditions, with the same Bit Rate and Bandwidth and Power constraints, we are going to improve the number of relays by 2, compared to our simpler Coding Scheme! So, our Coding scheme is good enough under these conditions.
We realized several simulations on the designed Turbo code to verify if the decoder was well implemented by looking at the evolution of the Bit Error Rate in function the number of iterations. To this end, we just had to perform soft decoding at the end of each iteration to observe that the decoded message was getting closer and closer to the initial message when the number of iteration was increasing.
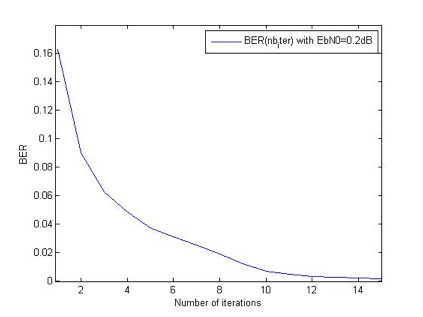
On this curve, we can see that the BER decreases exponentially and approach 0 as the number of iteration increases.
d) Transmission:
Using the loaded LONG-RANGE RECONNAISSANCE IMAGER (LORRI), loaded telescope, our satellite probe will achieve a resolution of 1024*1024 pixels. With true color 24 bits/pixels we obtain an image size of 3.145728 Mo. Since There will be a lot of repetition in the images that will be sent by the probe (open space) we are going to assume that by using the ZIP algorithm( lossless compression) we can compress it to 1/3 of its initial size. Hence, with the chosen bit rate of R=20bps, we will send an image in 4 days. We have designed the probe, with some advanced criteria of image selection and reasonable storage capacity. It will first take several pictures and select the most interesting ones, using detection algorithms. During the transmission, the closest Relay will direct its Antenna using Gyroscopic Mechanism to acquire the data, once the transmission acquired it will process and re-amplify the data to the closest Relay and Return to its listening Position.
