Propulsion Systems
Numerical Simulation and Data Inputs
The numerical Euler Explicit Method has been implemented on Matlab with the following parameters:
- Initial spacecraft Velocity relative to the Sun :
V0=42km.s-1
(this velocity is the composition of the Earth and the launcher velocity 29km.s-1 and 13km.s-1 respectively) - Sun Mass : Msun=1.989.10-30 kg
- Gravitational Constant : G=6.67.10-11 USI
- Flow rate for the 1st stage acceleration : α1=-100 g.s-1
- Flow rate for the 2nd stage acceleration : α2=-100 g.s-1
- Flow rate for the phase deceleration: α3=-100 g.s-1
- Specific Impulse during the 1st stage acceleration: Isp1=550.103s
- Specific Impulse during the 2nd stage acceleration: Isp2=450.103s
- Specific Impulse during the deceleration phase: Isp3=330.103s
- Fuel Mass for 1st stage acceleration : Mfuel1=700t
- Fuel Mass for 1st stage acceleration : Mfuel2=300t
- Fuel Mass for 1st stage acceleration : Mfuel3=250t
- Nuclear Reactor Power : P=265GW
- Dry Mass 1st stage : Md1=100t
- Dry Mass 2nd stage : Md2=50t
- Payload Mass : Md2=25t
- Time step : h=800
- Iteration number : 108
Numerical simulation results
The simulation results are written as follows:
- acceleration phase duration : 116 days
- 1st stage acceleration phase duration : 81 days
- 2nd stage acceleration phase duration : 35 days
- deceleration phase duration : 29 days
- Voyage duration : 485 years 3months
- Maximum speed : 6,500 km.s-1
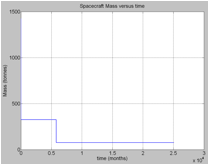
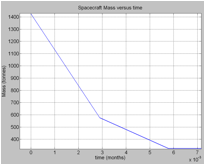
Fig.4: Spacecraft mass versus time. (a)Mass evolution during the whole voyage.(b) Mass evolution during the acceleration phase.
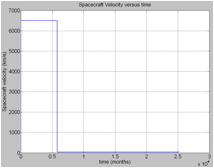
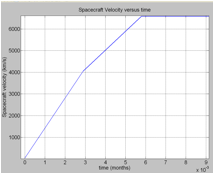
Fig.5: Spacecraft velocity versus time. (a)Velocity evolution during the whole voyage.(b) Velocity evolution during the acceleration phase.
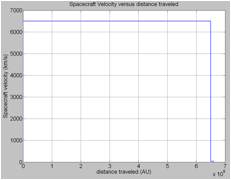
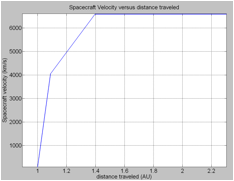
Fig.6: Spacecraft velocity versus distance traveled. (a)Velocity evolution during the whole voyage.(b) Velocity evolution during the acceleration phase.
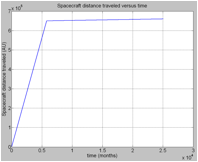
Fig.7: Spacecraft distance traveled versus time. (a) Distance traveled evolution during the whole voyage.
For details, please see the Matlab code.
Results Interpretation:
This propulsion system enables us to send a satellite to the Epsilon Eridani system in about 485 years. Nevertheless, we notice the power required to obtain such a performance is equal to 265GW and this number does take into account the thermal losses due to heat conduction. Nowadays, commercial nuclear plants may provide up to 10GW of power. From then on, setting up a 265GW nuclear reactor in a spacecraft is currently not possible without significant breakthrough in the nuclear area.