Propulsion Systems
Trajectory Analysis
To determine the amount of Hydrogen required achieving the entire voyage, we divide this problem into three distinct sub problems with respect to the Phase 1, Phase 2 and Phase 3.
Phase 1 is very critical insofar as it consists in leaving the solar system with a sufficient velocity to reduce the voyage time in the Milky Way. Since the amount of Hydrogen required to complete this travel is huge, we will consider a two-stage spacecraft which will split during the acceleration phase. The propulsion system provides continuous propulsion as long as the spacecraft is located in the Solar system. During the three phases, we consider a very simplified one dimensional model where the spacecraft only interacts with the Sun and the Epsilon Eridani star. By considering a one dimensional problem, a vectorial mechanical problem is converted into a scalar problem. After this first phase, the remaining amount of fuel in the reservoir’s spacecraft needs to be sufficient to ensure the deceleration phase (phase 3).
Classical mechanic and spacecraft motion:
We assume the Heliocentric referential as a Galilean referential. Both the spacecraft and the fuel stocked in the spacecraft form part of the mechanical system S:
S={spacecraft, fuel contained in the spacecraft}
From then on, the mass of the S is a function of time M(t). The system S undergoes both the Sun attraction and the Eridani star attraction Fsun and Feridani :
| (1) |
| (2) |
G=6.67.10-11m3.kg-1.s-2 : Gravitational constant
Ms= 2.1030kg : Mass of the Sun
M(t): Mass of the spacecraft
r: distance from spacecraft to the Sun
Reridani: distance from the Sun to the Eridani Star
Since the mass of the system varies, Newton's second law cannot be applied directly. Instead, the general equation of motion for a body whose mass m varies with time is written as follows:
![]()
(3)
Where P is the system momentum and ,Vp.is the effective exhaust velocity.
The spacecraft behavior is illustrated between two very close moments Fig.1.
Fig.3 : Representation of the speed evolution at time t and at time t+dt
The fuel debit flow α is a negative constant and the system mass is a decreasing linear function of time written as follows:
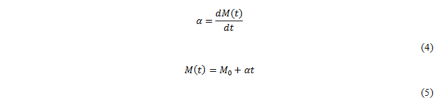
Finally, Newton second’s Law is written:
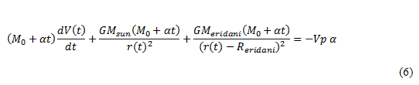
We notice (5) is a second-order nonlinear differential equation. The numerical Euler Explicit Method is used to solve it.
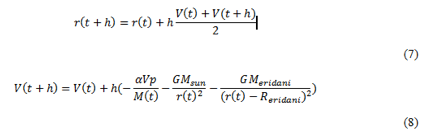
We notice the thrust force is commonly written as follows:

Where Isp is the specific impulse in seconds and ,g0. is the terrestrial gravitational constant.
Propulsion phases description:
Phase1
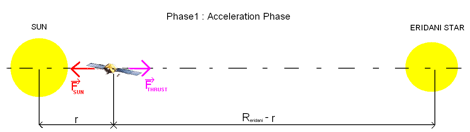
The phase 1 is the acceleration phase. Actually, we may divide into two sub phases this acceleration phase as Spacebuster is a two-stage spacecraft with distinct thrusts during each sub phase.
The first stage would operate for two years, taking the spacecraft to 7.1% of light speed and then after it was jettisoned the second stage would fire for 1.8 years, bringing the spacecraft up to about 12% of light speed.
During the phase 1, the interaction between the spacecraft and the Eridani are negligible.
Phase 2:

The propulsion sytem does not accelerate the spacecraft any more. It only controls and corrects the spacecraft trajectory. During this phase, the spacecraft interactions with both Eridani Star and the Sun are negligible.
Phase 3

The last phase is a decelaration phase. The Eridani star attraction cannot be neglected during this phase.