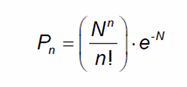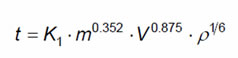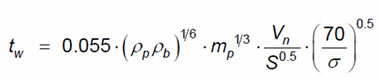MICROMETEORITE ENVIRONMENT

Characterization of Micrometeoroid Environment

Along with natural space dust and micrometeorites there's also been an increase in manmade space debris. Impacts from these small particles can be dangerous if their velocity is extremely high. The average density and velocity of micrometeoroids are 0.5 g/cm³ and 20 km/sec respectively and space debris or manmade debris is 2.8 g/cm3 and 10 km/sec. The micrometeoroid and orbiting impact damage recording system was implemented after the Columbia space shuttle accident of 2003 by the University of Dayton Research Institute. This study was conducted at LEO to monitor the space craft's wing and impacts that it encountered. This was deployed on the International Space Station to conduct the study on micrometeoroid impacts. 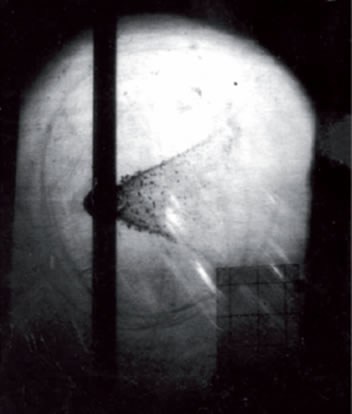Micrometeoroid impacts have been observed frequently in space including on STS-115 Atlantis. Also in the X-ray telescopes aboard the XMM-Newton observatory during revolution #156 more than 30 of the 150,000 pixels of the 6cmx6cm array lit up because damage to the mirror causing changes to the focal plane picked up by the pn-CCD detector array on board.

Figure E1. MISSE 6 On-Orbit Configuration

Current Knowledge of Micrometeoroid Impact Probability on Hardware

Because of this the probability that such events is dependent on the concentration of particles which determines the probability over a set area that a material may have an impact in orbit. The probability of impact over a given area is also known as the micrometeoroid fluence and there are many models that express this fluence levels shown here is the "Grun" flux model.

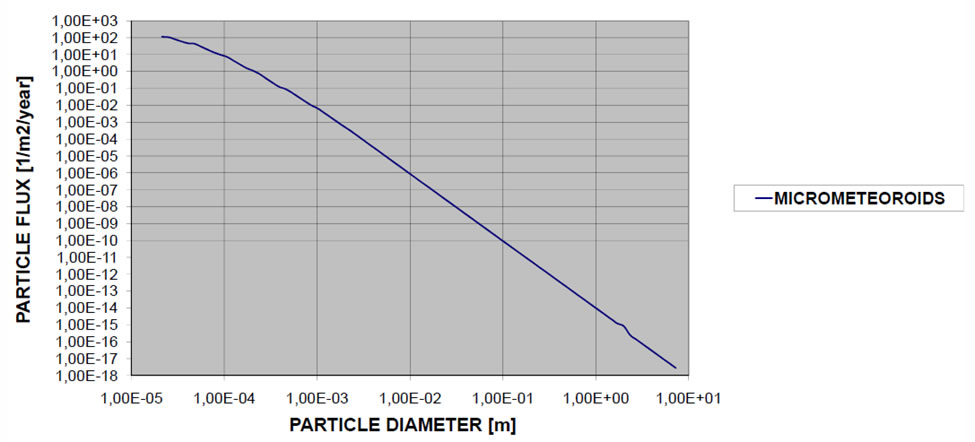
The total number of impact N is linked to:

The Probability of having n impacts over an area A follows the Poisson distribution bellow. Where P₀ would be the probability of having a single impact, P₁ would be the probability of having 1 impact and so on.

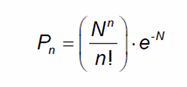
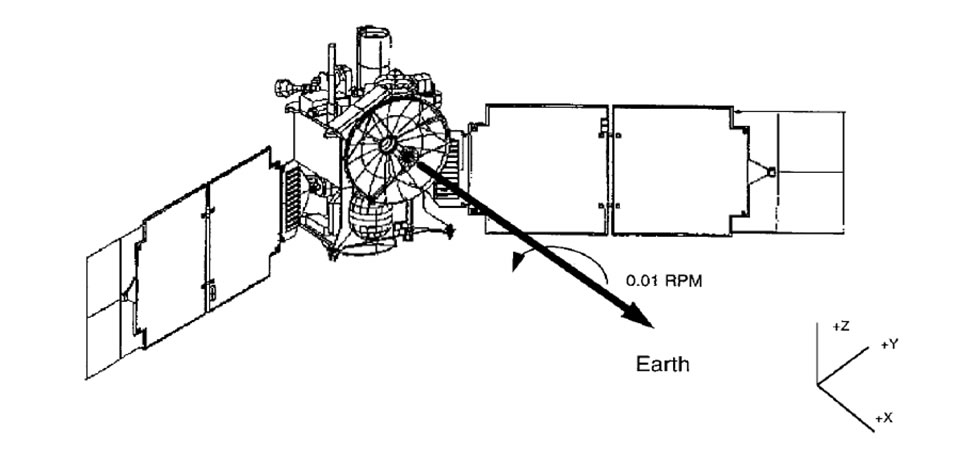
Also the leading edge of the orbiting satellite has a higher rate of impact then the trail side and so therefore must have better protection. Figure bellow shows the Mars Global Surveyor (MGS) project. The fluences for each surface were calculated. The side that faced the Mars orbiting velocity the +Y side. Since this is the leading edge it was calculated to have 20 times larger flux than the trailing edge of the space craft.

Figure E2. Orientation of MGS

For orbiting the earth the Grun model must take into account the earth shielding factor, the gravitational focusing factor increasing the flux, and the directional factor taking into account of the orbital orientation and velocity of the orbiting surface. NASA has additional to this model broken the impact particle into 2 categories; the debris or manmade particles with the micrometeorite flux. As it can be seen the micro meteoroid has a much wider velocity distribution than the manmade debris.

Damage Models of Impact

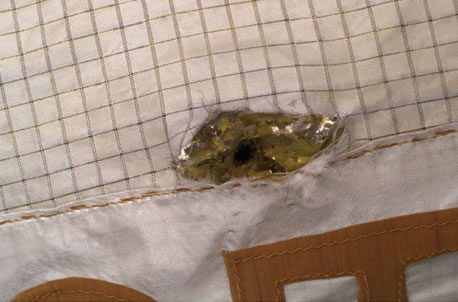
These impacts occur at hypervelocity mode or the particles exceed the sound propagation velocity in the material. This causes damage much greater then subsonic impacts. Due to this great impact the particle can cause the material to melt and/or vaporize causing a pressure wave which one or more of the fallowing damages, surface damage, spalling or punching also see supplementary photos to the right. Structural damage can be seen in penetration of spacecraft walls, penetration of pressurized vessels such as fuel tanks, cutting of cable and other electronic interconnects.

Impact Cone of Material

Single Wall Model or Front Wall

The Fish-Summers Equation can express the thickness needed for a single wall as long as the projectile material is aluminum and the plate material is magnesium-lithio, aluminum, copper-beryllium alloys and the impact velocity is from 0.5 to 8.5 Km/s. According to this model the plate thickness t (expressed in cm) is proportional to the particle mass m (g), the particle density p (g/cm³) and the impact velocity V (Km/s) as shown in the equation:

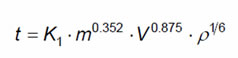
Where K1 is a constant depending on the plate material and is around 0.57 to 0.7. This equation gives the minimum value of t needed to avoid spalling

Double Wall Model or Trailing Wall Model

Under the same conditions as above the trailing edge of the spacecraft wall minimum thickness needed can be expressed by the bellow equation:

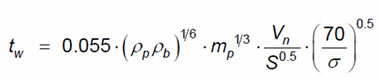
• t_b is the bumper thickness (cm)
• ρ_p is the particle density (g/cm³)
• ρ_b is the bumper density (g/cm³)
• m_p is the particle mass (g)
• S is the distance (cm) between the bumper and the rear-wallmper and the rear-wall
• σ is the rear-wall yield stress (ksi)

Conclusion

The lack of consider micrometeoroids on a space mission especially in the size and scale of the space solar power would be extremely costly. It is very likely that an event of some significance would impact one of the orbiting satellites and possibly more causing a catastrophic failure. In addition to this, the system performance would be degraded by a percentage related to the flux patter in the orbiting path and the duration of the mission. This will be critical because in order to achieve profitability the satellites must stay operational for at least 10 years to break even. With the above information care should be taken in the design of components protecting them. Also enough margins in the solar power arrays should be implemented to maintain adequate power for the satellite. There are in existence several ground test facilities that are capable of testing the required material needed for spacecraft protect. They use a Van De Graaff Accelerator or the Light Gas Gun. These methods have been used for testing such missions as Pegasus, Explorer 16, Explorer 23, HEOS 2, Pioneer 8, and Pioneer 9.