An interplanetary voyage to Venus requires the consideration of three major bodies: Earth, Sun, and Venus. The best approach to solving a problem of this complexity is to use the method of patched conics [1]. This method defines each major body of gravitational attraction as a Sphere of Influence (SOI).

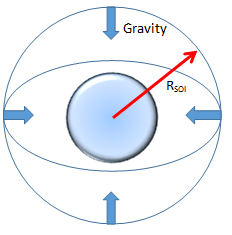
Sphere of Influence

The mission is then broken into a series of two-body problems to simplify the analysis [2]. Using this technique, there are three stages associated with the mission to Venus.

    Stage 1: Space Craft and Earth (SOI)
    Stage 2: Space Craft and Sun (SOI)
    Stage 3: Space Craft and Venus (SOI)

Stages 1 and 3 are hyperbolic orbits. Stage 2 is a transfer between Earth orbit and Venus orbit. This requires a fuel efficient orbit, so a Hohmann transfer is selected for this transfer. The aphelion in this instance is the Earth orbit location and the perihelion is the Venus orbit location. Using the patched conic method simplifies the trajectory analysis and allows the determination of the total velocity change a rocket needs to achieve its journey to Venus, which is called the total Δv.

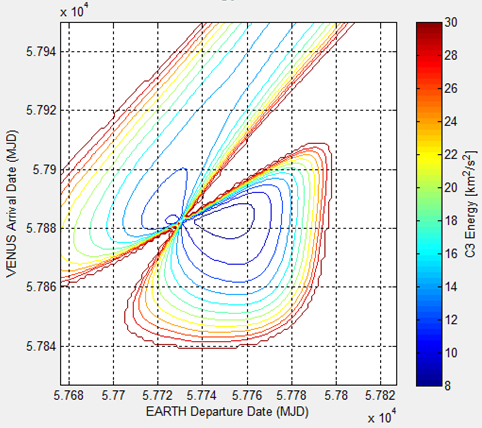
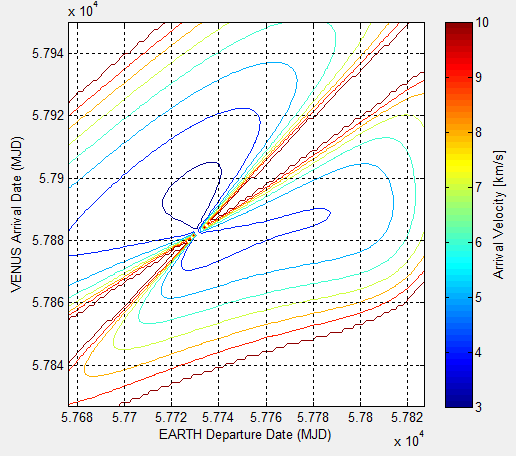
The launch window is the next vital piece of information. The space craft must reach Venus's orbit at the same time as Venus, which presents an opportunity for launch approximately every 19 months. Selecting the proper date is a tradeoff between primarily three factors: Total Δv, time to achieve final orbit, and the final velocity at the destination planet. Total Δv provides a quantitative amount of the effort used during the entire trajectory, and is used for selecting the rocket(s) required for launch. A mission to measure the seismic activity of Venus is not entirely time critical, however, the longer an object is on its trajectory in space, the more power that is used for the electronics . In addition to this, there is also a risk of damage from objects in space that may contact the vehicle. Therefore, it is best to consider time as a tradeoff when determining the launch window. The last major factor to consider is the final velocity of the space craft when it arrives at Venus. There will be two parts to the arrival: the satellite and the deployed section that will enter the atmosphere of Venus. It will therefore be necessary to decrease the speed of the craft so that it will enter Venus's orbit and not just fly by. In order to accomplish this, a technique called aerobraking with the aid of a series of small rocket burns will be used to set the satellite in proper orbit. Aerobraking uses the atmosphere of Venus to slow down the space craft to an acceptable velocity required to enter the orbit.

The most common form of launch is called a “prograde” launch, which uses the rotation energy of the Earth to assist in launching the space craft. When launching to an inner planet in relation to Earth, it is better to launch in a “retrograde” fashion. This type of launch will continue to follow Earth's revolution at the beginning, but at a slower speed than a prograde type. This will be a daylight launch from Cape Canaveral, Florida.

Lambert's problem is the algorithm that was utilized in the trajectory solver. This solver ignores all bodies except for the Sun when analyzing the transfer orbit between planets. Considering the tradeoffs discussed above, a decision was made to launch the satellite on January 15, 2017 [3]. This trajectory has an arrival date on May 7, 2017, spending just 112 days on the journey. The location of the planets at the departure date and the space craft trajectory is shown in the figure below. When the space craft arrives, Venus will be at the location of the X.

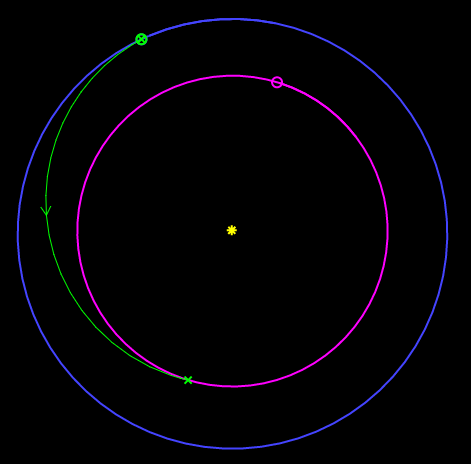Earth's Orbit - Blue Space Craft's Orbit - Green Venus's Orbit - Purple

A pork chop plot [4] of this trajectory further verifies this launch date. This plot shows the C3 energy required for launch over a range of Modified Julian Dates (MJD). This is the square of the hyperbolic excess velocity, which is the vector difference between Earth’s velocity and the heliocentric orbit’s velocity. This is related to Δv and the amount of energy required to achieve orbit. The dates above are in the optimal region of the plot highlighted below with a red X. The C3 for the mission is 8.5km2/s2. The Δv required to inject from low earth orbit to the transfer orbit is 3.61km/s. The total Δv required from the departure to the arrival at Venus is 4.36km/s.

The arrival velocity was also found using the program. The plot below shows the information. The arrival velocity is approximately 4km/s with the given launch and arrival dates.

A circular orbit was chosen for the satellite in this mission. The satellite will reside at an altitude of 250km with an inclination of 60⁰ so that it will be close to the Ishtar Terra landmass (70.4⁰N, 27.5⁰E). This will mean that the satellite makes one complete revolution about Venus every 1.4806 hours (5530 seconds) in Earth time.

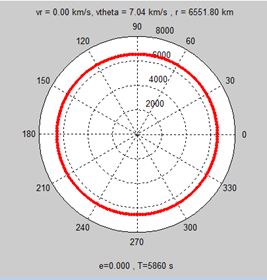
Satellite Orbit