The Location Algorithm
Our Location Algorithm provides two techniques by which the astronaut can wander around the Lunar Lander and reach back safely to the Lander even from a far off, non line of sight location on the Moon. For details of our algorithm, read on.
Choosing Received Signal Strength (RSS)
The two most common methods for performing multilateration are time difference of arrival (TDOA) and received signal strength (RSS). (Frequency difference of arrival isn’t as common or as practical because we can’t assume that enough motion is occurring to generate the necessary Doppler.) We have chosen to discard time difference of arrival because the distances are so small. The Communications page established that the RFIDs are only useful at 9.79 meters, which translates to 32.7 ns. As Pratt explains on page 464, a typical crystal oscillator that the astronaut’s electronics would use has an accuracy of 1 in 105 or 1 in 106. This translates to a uncertainty of 300 meters, which is 30 times larger than the RFID signal range!
Trilateration
Trilateration is simple enough to visualize:
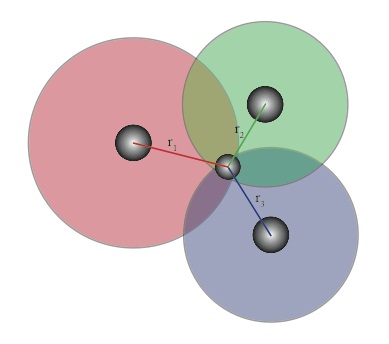
Figure 1: Trilateration.
However, in the case of our astronaut the 3rd circle is 2km of coverage from the lander. Thus, we are only ever concerned with the weaker of the two nearest RFIDs. For the case of the lander and the first two RFIDs we get plots like this:
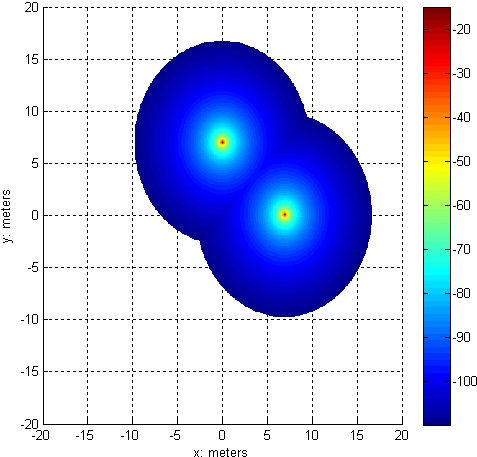 | 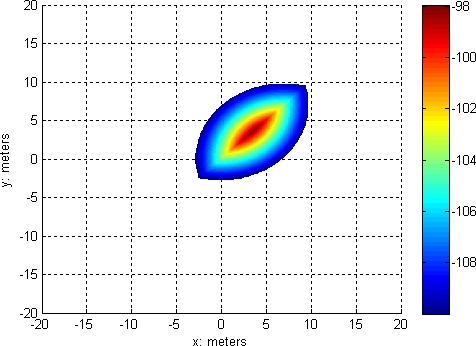 |
| Figure 2: The maximum received signal strength, ignoring the lander. | Figure 3: The minimum received signal strength |
In other words, the astronaut knows his exact location when he is within the colored region of the second graph because trilateration can be performed in that region. The diagonal shape of the second graph is not a surprise; the diagonal line through the second graph is the locus of points equidistant from the two RFIDs.

In other words, the astronaut has the largest signal strength when he walks in a straight line between the two RFIDs.
Wandering
In principle, the astronaut can place the 3rd RFID anywhere in the colored region of the second graph to extend the region in which trilateration is possible. Thus, the astronaut is able to wander about the lunar surface, place RFIDs as he walks, and always know where he is. (Note that he will know where he is relative to the nearest RFIDs. His computer will have to recursively keep track of where the nearby RFIDs are relative to the lander. That’s where the information in the tag about the distance from the lander comes in handy) However, if all of the RFIDs are referenced relative to previous RFIDs, then how does the astronaut establish the initial conditions: the axes and the angles of the first two RFIDs? First, an assumption is made for the first RFID: if there are no other identifying features on the moon, then we can declare that the first RFID is on the positive x-axis. Since the received signal strength (RSS) gives us the radius of both the 1st and 2nd RFIDs, the only thing left is the angle of the 2nd RFID relative to the x-axis that we just defined. There are two options for this. If the astronaut knows the general direction that he traveled from the 2nd RFID to the 3rd RFID then the ambiguity shown in the locus diagram can be resolved, allowing for bilateration. However, if the astronaut doesn’t trust his bearings then a protractor will be necessary:

Even though the astronaut can wander somewhat freely, it is still useful to have algorithms for tasks and objectives:
Traveling in a straight line
Cover the most area possible near the lander
The Matlab code for both algorithms
