Traveling in a straight line
If the astronaut sees something interesting off in the distance then he might choose to travel in a straight line towards it. In that case, he merely travels along the locus as previously indicated, adding new RFIDs on either side of the locus as he goes. Notice that the colorbars are different for the two plots.
 |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
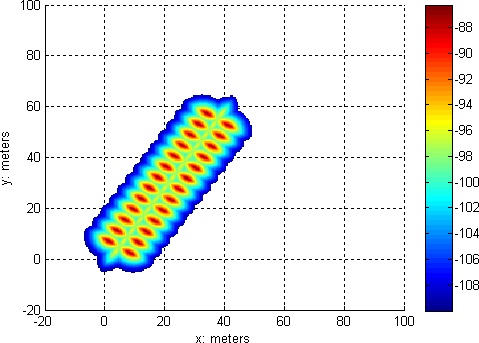
| Figure 1: The maximum received signal strength, ignoring the lander | Figure 2: The minimum received signal strength of the 3 nearest transmitters | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Figure 3: The maximum received signal strength,including the lander | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Each pair of RFIDs has its own locus, and the astronaut's portable computer will keep track of the locus of the most recent pair to show the astronaut where to place the next pair of RFIDs.
There are two wrinkles in this simplistic algorithm. The first complication is the tradeoff between path width and accuracy. As explained on the Communications page, the pair of RFIDs have to be no more than 9.79 meters apart. Using this maximum width means the RFID pairs have to be very close together along the locus direction. By contrast, an arbitrary pair width of 3.34 meters yields a spacing of ~9.2 meters between the RFID pairs. It should be noted that this narrow pair width would require ~450 RFIDs to reach 2 km. This is unavoidable since the useful radius of the RFIDs is so small.
The other complication is measurement error. At the edge of the 2 km range, the isosceles triangle would have a lander angle of 90-atan(2000/(9.79/2))=0.14°. If we assume that the system only has an accuracy of 0.1° then the system would barely be able to tell that there is a triangle and not just a straight line! In other words, the further the astronaut gets from the lander the more severe a small angle error becomes.
As a final side note, if the astronaut needs to curve to avoid a terrain obstacle, such as a crater, then he can do so simply by deviating slightly from the locus:
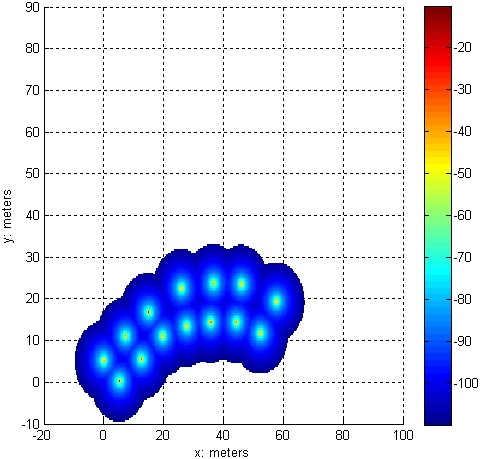
Figure 4: Deviating from a straight line path.
Cover the most area possible near the lander
The Matlab code for both algorithms
